Задача про порты соедененые каналами (графы, min, max?)

[perelman]

В некотором государстве порта соединены морскими каналами. Длина любого канала менее 500 км. Из любого порта в любой другой можно попасть на судне, преодолев путь по каналам менее 500 км. Когда один канал закрыли на дноуглубительные работы, выяснилось, что из любого порта можно дойти в любой другой по каналам, которые остались. Докажите, что это возможно преодолев путь не более 1500 км.
Помогите решить до пятницы :)

[Shadow]

Еще надо уточнить, что все каналы - отрезки.

[Null]

Попробуйте так: Пусть удаляемый канал AB. Разобьем все Порты на 4 группы:
$X\in S$ - кратчайший путь от A до X содержит AB и кратчайший путь от B до X содержит AB,
$X\in S_A$ - кратчайший путь от A до X не содержит AB, а кратчайший путь от B до X содержит AB.
$X\in S_B$ - кратчайший путь от A до X содержит AB, а кратчайший путь от B до X не содержит AB.
$X\in S_{AB}$ - кратчайший путь от A до X не содержит AB и кратчайший путь от B до X не содержит AB.

1. $A\in S_A$, $B\in S_B$
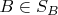
2. Если $S_{AB}$ непусто, то задача решена.
3. S - пусто.
4.Кратчайший путь между элементами из $S_A$ не содержит AB.
Кратчайший путь между элементами из $S_B$ не содержит AB.
5. Возьмем ребро CD, $C\in S_A, D\in S_B$. Пусть $A-CD-B$ искомый.

Это план решения.