Требуется доказать, что для любых

точка

на графике лежит не выше хорды, соединяющей точки

и

. А исходим мы из того, что это утверждение верно хотя бы для

(и, естественно, для

или

).
Доказывать достаточно для

, где
![$\theta_n\in[0;1]$ $\theta_n\in[0;1]$](https://dxdy-04.korotkov.co.uk/f/f/6/8/f686a49e803cc58c8b0762a90a0238f782.png)
-- конечная

-разрядная двоичная дробь с произвольным

. Поскольку любое вещественное
![$\theta\in[0;1]$ $\theta\in[0;1]$](https://dxdy-01.korotkov.co.uk/f/c/7/c/c7c58cf02baa74352e7a62b20944167982.png)
является пределом таких
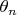
, и если неравенство верно для них -- в силу непрерывности оно переносится и на предельную

(а тот или иной предельный переход проводить в любом случае придётся, поскольку непрерывность существенна: не будь её, утверждение было бы неверным).
Для конечных двоичных дробей геометрически всё очевидно, а формально обосновывается индукцией по

: если предположить, что утверждение верно для всех

при некотором

, то тем более оно верно для любого

, поскольку любое

лежит ровно посередине между какой-то парой соседних

или совпадает с одним из

.



