Факториальная дробь

[Dave]

(Оффтоп)

Дам своё решение, на случай, если эта задача кого-то заинтересует. Старался расписать всё максимально подробно и дать замкнутое доказательство, без ссылок на другие источники, чтобы было понятно любому школьнику. Утверждение 5 в нижеприведённом доказательстве может быть рассмотрено как отдельная задача.

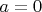
Если $b=0$, то подстановка $n=m=2$ говорит о том, что ни $a=0$, ни $a=1$ не подходят для того, чтобы дробь всегда была целой. В случае же $a \geqslant 2$: $\frac {(an)!(am)!} {n!m!(bn+m)!(n+bm)!}=\frac {(an)!} {(2n)!} \frac {(2n)!} {n!n!} \frac {(am)!} {(2m)!} \frac {(2m)!} {m!m!}=\frac {(an)!} {(2n)!} C_{2n}^n \frac {(am)!} {(2m)!} C_{2m}^m$ - всегда целое число, как произведение четырёх целых чисел. Значит для случая $b=0$ утверждение доказано.

Теперь рассмотрим случай $b \geqslant 1$. Подстановкой $n=m=1$ сразу убеждаемся, что в случае $a \leqslant b$ дробь будет нецелой, равно как и неравенство не будет справедливым. Значит остаётся рассмотреть случай $a>b \geqslant 1$.

Для любого натурального $n$ и простого $p$ обозначим через $W_p(n)$ степень, с которой $p$ входит в разложение $n$ на простые множители.

Утверждение 1. Если $n$ и $m$ - натуральные числа, то $n$ делится на $m$ тогда и только тогда, когда $W_p(n) \geqslant W_p(m)$ для любого простого $p$. (Очевидно).

Утверждение 2. Если $n$ и $m$ - натуральные числа, а $p$ - простое число, то $W_p(nm)=W_p(n)+W_p(m)$. (Очевидно).

Утверждение 3. Если $z$ - неотрицательное целое число, а $p$ - простое число, то $\displaystyle W_p(z!) = \sum_{i=1}^{\infty} \left[ \frac z {p^i} \right]$.
Этот известный факт, называемый иногда формулой Лежандра, может быть получен индукцией по $z$, с использованием предыдущего утверждения для $n=(z-1)!$, $m=z$.

Зафиксируем натуральные числа $a$ и $b$ и рассмотрим функцию двух действительных переменных $F(x,y)=[ax]+[ay]-[x]-[y]-[bx+y]-[x+by]$.

Утверждение 4. Число $(an)!(am)!$ делится на число $n!m!(bn+m)!(n+bm)!$ для всех неотрицательных $n$ и $m$ тогда и только тогда, когда для всех таких $n$ и $m$ и любого простого $p$: $\displaystyle \sum_{i=1}^{\infty} F\left(\frac n {p^i},\frac m {p^i} \right) \geqslant 0.$
Заметим, что в вышеуказанной сумме, равно как и в формуле Лежандра, только конечное число слагаемых отлично от нуля. Согласно утверждению 1, делимость равносильна неотрицательности разности $W_p((an)!(am)!)-W_p(n!m!(bn+m)!(n+bm)!)$ для любых неотрицательных $n$, $m$ и простого $p$. Согласно утверждению 2, эту разность мы можем расписать как $W_p((an)!)+W_p((am)!)-W_p(n!)-W_p(m!)-W_p((bn+m)!)-W_p((n+bm)!)$, а, согласно утверждению 3, как $\sum\limits_{i=1}^{\infty} \left( \left[ \frac {an} {p^i} \right] + \left[ \frac {am} {p^i} \right] - \left[ \frac n {p^i} \right] - \left[ \frac m {p^i} \right] - \left[ \frac {bn+m} {p^i} \right] - \left[ \frac {n+bm} {p^i} \right] \right)$, наконец, используя определение функции $F(x,y)$, переписать как $\sum\limits_{i=1}^{\infty} F\left(\frac n {p^i},\frac m {p^i} \right)$.

Утверждение 5. Если $a$ и $b$ - натуральные числа, такие, что $a>b+\sqrt {b}$, то для любых целых $n$ и $m$:

$$n+m \leqslant \max \, \left\{ \frac {an-1} b , \, am-b, \, 0 \right\}.$$

Для доказательства обозначим $c=a-b > \sqrt {b} >0$, $r=bm-cn$ и рассмотрим 3 возможных случая:
а) $r \leqslant -1$. Тогда $bm-an+bn \leqslant -1$, $bn+bm \leqslant an-1 $ и $n+m \leqslant \frac {an-1} b$.
б) $r \geqslant 0, \, m \geqslant 1$. Тогда $-n \geqslant - \frac {bm} c$ и, обозначив $v=am-b-n-m$, имеем: $ v \geqslant am-b-\frac {bm} c -m = m((b+c)-\frac b c -1)-b=m((b-1)+(c-\frac b c))-b$. Т.к. $b \geqslant 1$, a $c > \frac b c$ , то $(b-1)+(c-\frac b c)>0$ и, т.к. $m \geqslant 1$, то $v \geqslant 1 \cdot ((b-1)+(c-\frac b c))-b = (c-\frac b c)-1>-1 $. Но число $v$ - целое, поэтому $v \geqslant 0$ и $n+m \leqslant am-b$.
в) $r \geqslant 0, \, m \leqslant 0$. Тогда $cn \leqslant bm \leqslant 0$, откуда $n \leqslant 0$ и $n+m \leqslant 0$.

Утверждение 6. Для любого действительного $x$ и целого $n$: $[x+n]=[x]+n$. (Очевидно).

Утверждение 7. Если $a$ и $b$ - натуральные числа, такие, что $a>b+\sqrt {b}$, то для всех неотрицательных $x$ и $y$: $F(x,y) \geqslant 0$.
Действительно, т.к. $b \geqslant 1$, то $a-b>\sqrt {b} \geqslant 1$ и $a-b \geqslant 2$. Пусть $x_1=\{x\}$, $y_1=\{y\}$. Тогда $x=x_1+[x]$, $y=y_1+[y]$ и из утверждения 6 следует, что мы можем разложить каждую целую часть, входящую в $F(x,y)$, по типу $[ax_1+a[x]]=[ax_1]+a[x]$. Получим, что $F(x,y)=F(x_1,y_1)+(a-b-2)([x]+[y]) \geqslant F(x_1,y_1)$ и нам достаточно доказать, что $F(x_1,y_1) \geqslant 0$, если $x_1 \in [0,1)$, $y_1 \in [0,1)$.
Пусть, для определённости, $x_1 \geqslant y_1$. Пусть также $k=[ay_1]$, $x_2=x_1-\frac k a$ и $y_2=y_1-\frac k a$. Тогда, т.к. $ax_1 \geqslant ay_1 \geqslant k$, то $x_2 \geqslant 0$, а, т.к. $ay_1 \geqslant k > ay_1-1$, то $0 \leqslant y_2 <\frac 1 a$. Обозначим $n=[bx_2+y_2]$, $m=[x_2+by_2]$ и заметим, что $\frac {b+1} a k \leqslant k$, поэтому $[bx_1+y_1]=[bx_2+y_2+ \frac {b+1} a k] \leqslant [bx_2+y_2+k]=n+k$ и $[x_1+by_1]=[x_2+by_2+ \frac {b+1} a k] \leqslant [x_2+by_2+k]=m+k$. В то же время, $[ax_1]=[ax_2+k]=[ax_2]+k$, а $[ay_1]=[ay_2+k]=[ay_2]+k=k$. Теперь применим утверждение 5 к вышеуказанным $n$ и $m$. Поскольку $\frac {an-1} b \leqslant \frac {a(bx_2+y_2)-1} b =ax_2+ \frac {ay_2-1} b<ax_2$, $am-b \leqslant a(x_2+by_2)-b=ax_2+(ay_2-1)b<ax_2$ и $0 \leqslant ax_2$, то максимум в правой части утверждения 5 будет не больше $ax_2$. Из того, что целое число $n+m$ не больше $ax_2$, следует, что и $n+m \leqslant [ax_2]$. Итак, $[ax_1]+[ay_1]=[ax_2]+2k \geqslant n+m+2k \geqslant [bx_1+y_1] +[x_1+by_1]$, что и требовалось доказать.

Утверждение 8. Если $a$ и $b$ - натуральные числа, такие, что $b< a \leqslant b+\sqrt {b}$, то существуют такие интервалы $I_x \subset (0,1)$ и $I_y \subset (0,1)$, длиной не менее $\frac 1 {2ab^2}$, что для любых $x \in I_x$ и $y \in I_y$: $F(x,y)<0$.
Действительно, если $c=a-b$, то $1 \leqslant c \leqslant \sqrt {b}$ и, полагая $k=\left[ \frac b c \right]$, в качестве требуемых интервалов можно взять

$$I_x=\left(\frac k b - \frac 1 {2ab}, \frac k b\right) \quad \text{и} \quad I_y=\left(\frac 1 a- \frac 1 {2ab^2}, \frac 1 a \right).$$

Тогда, если $x \in I_x$, а $y \in I_y$, то:
а) $ax<\frac {ak} b=\frac {(b+c)k} b=k+k\frac c b \leqslant k+\frac b c \frac c b=k+1$ и $[ax] \leqslant k$;
б) $ay<1$ и $[ay]=0$;
в) $x<1$ и $[x]=0$;
г) $y<1$ и $[y]=0$;
д) $bx+y>k-\frac 1 {2a}+\frac 1 a -\frac 1 {2ab^2} = k + \frac {b^2-1} {2ab^2} \geqslant k$ и $[bx+y] \geqslant k$;
е) $x+by>\frac k b - \frac 1 {2ab} + \frac b a - \frac 1 {2ab} = \frac {ka+b^2-1} {ab}$. Заметим, что $k> \frac b c - 1$, значит $kc \geqslant b-c+1$, стало быть $k \geqslant \frac {b+1} c -1$ и $b-k \leqslant b+1-\frac {b+1} c = (1-\frac 1 c)(b+1) \leqslant (1-\frac 1 {\sqrt {b}})(b+1)$. Отсюда $a(b-k) \leqslant (b+\sqrt {b})(1-\frac 1 {\sqrt {b}})(b+1)=b^2-1$, поэтому $ab \leqslant ka+b^2-1$, т.е. $x+by>1$ и $[x+by] \geqslant 1$.
Резюмируя всё вышесказанное, находим, что для указанных $x$ и $y$: $F(x,y) \leqslant k+0-0-0-k-1<0$.

Теперь, возвращаясь к задаче, видим, что утверждения 4 и 7 немедленно дают доказательство в случае $a>b+\sqrt {b}$. В случае же $b< a \leqslant b+\sqrt {b}$ выберем гарантируемые утверждением 8 интервалы $I_x$ и $I_y$, а также какое-нибудь простое число $p$, большее, чем $2ab^2$. Тогда интервалы $pI_x$ и $pI_y$ имеют длину больше $1$, стало быть, каждый из них содержит как минимум одно натуральное число, пусть это будут, соответственно, $n$ и $m$. Заметим, что, т.к. $I_x \subset (0,1)$ и $I_y \subset (0,1)$, то $n<p$ и $m<p$, поэтому каждое из чисел $an, am, n, m, bn+m, n+bm$ меньше $ap$, а значит, если мы его разделим на $p^i$, где $i \geqslant 2$, то получим число, меньшее, чем $\frac {ap} {p^2} = \frac a p < \frac a {2ab^2} < 1$. Поэтому $F\left(\frac n {p^i},\frac m {p^i} \right) = 0$ при $i \geqslant 2$. Что же касается $F\left(\frac n p,\frac m p \right)$, то, т.к. $\frac n p \in I_x$ и $\frac m p \in I_y$, то это число отрицательно. Значит, используя утверждение 4 и найденные $n$, $m$ и $p$, мы можем заключить, что при $b< a \leqslant b+\sqrt {b}$ дробь в условии задачи даёт нецелое число и доказываемое утверждение также справедливо. $\blacksquare$