From nested intervals property to least upper bound axiom

[gefest_md]

I want to prove the following theorem using nested intervals:

Цитата:

Every non-empty set of real numbers that is bounded from above has a least upper bound in the real numbers.

Hints:

Цитата:

(a) Suppose $A$ is a non-empty set bounded above by $M$. Then we can choose some $x\in A$. We can split the interval $[x,\ M]$ in half repeatedly. At each stage,
1) keep the right half of the split interval if it contains any elements of $A$;
2) otherwise, keep the left half.

b) Prove that the single element of $\cap[a_n,\ b_n]$ is least upper bound by contradiction

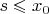
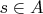
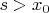
Suppose $x_0$ is the single real number, the intersection of all the intervals. And first I want to show that $s\leqslant x_0$, for all $s\in A$. Suppose there is $s>x_0$. I am thinking that I would be able to contradict 1) "keep the right..." if I could prove the existence of an interval with $x_0$ in left half, and $s$ in right half. Is it possible to prove this? Or I am on a wrong way?

[AGu]

Proving by contradiction is most probably suggested for the "least" part of the claim.
As regards the "upper bound" part, try using the fact (which can be proven by induction) that, for each $n$, there are no elements of $A$ above $b_n$.

[gefest_md]

AGu в сообщении #529428 писал(а):

As regards the "upper bound" part, try using the fact (which can be proven by induction) that, for each $n$, there are no elements of $A$ above $b_n$.

Also, I think it is necessary the following. If $[a_1,\ b_1]$ contains one or more elements from $A$, then, for all $n$, $[a_n,\ b_n]$ also contains one or more elements from $A$. This seems to me to be necessary when you prove that any upper bounds are not below $x_0$, mentioned earlier.


For the sake of completeness I add the following:

\begin{displaymath} \lim_{n\to\infty}(b_n-a_n)=\lim_{n\to\infty}\left[\frac{1}{2^{n-1}}(b_1-a_1)\right]= \lim_{n\to\infty}\frac{1}{2^n}\cdot\lim_{n\to\infty}2(M-x)=0\cdot2(M-x)=0\end{displaymath}

which is necessary to produce the single real number $x_0$, the intersection of nested intervals.