I want to prove the following theorem using nested intervals:
Цитата:
Every non-empty set of real numbers that is bounded from above has a least upper bound in the real numbers.
Hints:
Цитата:
(a) Suppose

is a non-empty set bounded above by

. Then we can choose some

. We can split the interval
![$[x,\ M]$ $[x,\ M]$](https://dxdy-03.korotkov.co.uk/f/6/0/7/607fa4a7224c05ba6d45b4556167817882.png)
in half repeatedly. At each stage,
1) keep the right half of the split interval if it contains any elements of

;
2) otherwise, keep the left half.
b) Prove that the single element of
![$\cap[a_n,\ b_n]$ $\cap[a_n,\ b_n]$](https://dxdy-01.korotkov.co.uk/f/0/0/1/00147619f463ab72b8442b257714ff8b82.png)
is least upper bound by contradiction
Suppose

is the single real number, the intersection of all the intervals. And first I want to show that
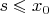
, for all
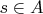
. Suppose there is

. I am thinking that I would be able to contradict 1) "keep the right..." if I could prove the existence of an interval with

in left half, and

in right half. Is it possible to prove this? Or I am on a wrong way?