Решений много.
1)Пусть

. Если
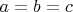
, то

квадрат, следовательно

нечетное


любое натуральное.
2) Пусть

. Тогда

квадрат. Если

нечетное, то решений нет, так как
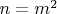
. Если

четное то

и

квадрат и

нечетное. Сводится к решению


. Тут еще налагается условие на

причем

-четное. Не знаю есть ли решение с

проверить

так же не просто.
3) Пусть

. Тогда

квадрат. Много решений вида

(можно брать

) с тем же уравнением Пелля. Много решений и

- четное

квадрат (хотя бы с тем же уравнением Пелля

.
4)

Тогда решений с нечетным с по видимому нет (в конкретных случаях доказывается легко, общий случай сводится к целым точкам на эллиптической кривой). Для четного

сводится к

квадрат. Случай

не имеет решений. Случай четного m и

не имеет решений.Случай

разбирается по модулю

. Тривиальное решение при

получается n=2. Есть конечное число решений, например

.



