Ну вот, и библиографические ссылки начинают появляться:

Spiral Fat Arcs – Bounding Regions with Cubic Convergence
Michael Bartoň, and Gershon Elber
Technion – Israel Institute of Technology, Haifa 32000, Israel
Received 17 August 2010; revised 25 October 2010; accepted 27 October 2010. Available online 4 November 2010.
Abstract
A bounding region for spiral curve segments shaped by two circular arcs, parts of the osculating circles at the spiral’s endpoints, and two lines is introduced. This bounding region, denoted Spiral Fat Arc (
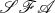
) is simple to construct and process, and shows a cubic approximation order to a given spiral curve.
Given a general planar parametric curve, it can be split at curvature extrema (and inflection points), solving for the parametric locations for which κ’ = 0 (and κ = 0), κ being the signed curvature field, to yield a set of spiral curves. Each of the spirals is then fitted with a bounding (
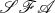
).
Finding the intersection locations of two free-form planar curves is a fundamental task in geometric computing and computer aided design, and can immediately benefit from this new (
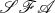
) bounding region. A recursive curve-curve intersection (CCI) algorithm that efficiently computes the intersection location of two parametric curves using (
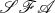
)s is also introduced.
Keywords: spiral; monotone curvature; curve-curve intersection; bounding regions; fat-arcs
Статью не читал (может, у кого-нть есть доступ?). Но многое сходится:
Cubic Convergence:
c) Количество узлов увеличено с 11 до 15. При увеличении количества точек в n раз ширина области уменьшается в n^3 раз.
"it can be split at curvature extrema (and inflection points), solving for the parametric locations for which κ’ = 0 (and κ = 0),"
Мы разбиваем кривую на достаточно малые отрезки-дуги следующим образом:
(1) выделяем вершины кривой; таким образом, кривизна на каждом участке будет монотонна, ...
Я, наоборот, подчеркиваю, что точки перегиба не нужны (это просто традиция, от которой писатели в этой области не могут отказаться):
... (будет там внутри перегиб или нет --- нам до лампочки); ...
"A bounding region ... shaped by two circular arcs, parts of the osculating circles at the spiral’s endpoints, ...:
Дуга
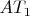
, часть бидуги
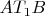
, имеет кривизну

, ту самую, что и наша оригинальная кривая в точке

.
Дуга
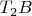
, часть бидуги
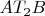
, имеет кривизну

, ту самую, что и наша оригинальная кривая в точке

.
Может, у кого-нибудь есть доступ?



