Пишу все аккуратно, чтобы вслучае ляпов меня исправили.
Длее, разберемься, что такое изометрии группы. Будем считать, что наше многообразие вложено в какое-то евклидово многообразие
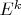
.
Рассмотрим гладкое отображение

, такое, что

.
Определение: Линейная оболочка величин

называется касательным пространством к

в точке

и обозначается

.
В группе существует выделенная точка

(единица группы), которая не изменяется при преобразовании

Это преобразование является внутренним автоморфизмом группы. Понятно, что такое преобразование порождает линейное отображение касательного пространства

Понятно, что

,

а значит,

является представлением группы

на линейном пространстве

. Тем самым мы задали отображение:

Правильно ли я понимаю, что каноническая метрика на

как-то связана с величиной
 -- Пн ноя 14, 2011 15:15:09 --
-- Пн ноя 14, 2011 15:15:09 --нет, неправильно.
Понял, понял... Не всякое многообразие, на котором группа действует транзитивно является многообразием этой группы всмысле данного выше определения. Например группа Пуанкаре

действует транзитивно на

, однако

не является многообразием группы Пуанкаре.
Тут

означает полупрямое произведение.
(Полупрямое произведение)
Как в

-е нарисовать знак полупрямого произведения?



