Спасибо за предложение рассмотреть в общем виде! Подскажите, верно ли предположение (как я понял, полное решение по правилам форума я как постановщик вопроса могу изложить...)
Рассмотрим два случая, пользуясь теорией остатков (конгруентностей, прошу простить, если написано неправильно, исхожу из правил украинской грамматики).
1) m - четное число, отличное от двух (т.к.

,
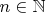
). Тогда несложно заметить, что:


...


...


Отметим, что k - нечетное. Ввиду этого

остается отрицательным. То есть:

Докажем, что

не исполняется равенство

. Предположим, что это так. Тогда

. Несложными преобразованиями легко получить

, что противоречит условию

.
Поэтому, когда m - четное, то данная сума на m не делится нацело.
2) Если m - нечетное число. Тогда

не является целым, но являются целыми

и

. Тогда аналогично:


...


...


Но тут ситуация будет выглядеть гораздо проще, чем в первом случае:

Поскольку

, то

.
Соответственно, поскольку сумма

не делится нацело на m, то и не делится нацело сумма

на число n.
Что и следовало доказать!
 -- 11.11.2011, 22:18 --Sonic86
-- 11.11.2011, 22:18 --Sonic86Огромное спасибо, сохраню на будущее!




