Поговорим о геодезических -- для разминки перед орициклами, а также потому, что орициклы ортогональны некоторому семейству геодезических.
Уравнение геодезических:

, где

.
Сравнивая с формулой для кривизны, которую привел
Padawan, видим, что кривизна геодезической равна нулю.
В Википедии (статья
Модель Пуанкаре) сказано:
Цитата:
Роль прямых выполняют содержащиеся в этой полуплоскости полуокружности с центрами на абсолюте и начинающиеся на абсолюте перпендикулярные ему лучи (то есть вертикальные лучи).
То есть утверждается, что геодезическими являются линии, изображаемые в модели как полуокружности

,
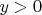
. (Вертикальные лучи рассматривать не будем.)
Вместо того, чтобы решать уравнение геодезических, я просто покажу, что данная в Википедии информация верна.
Рассмотрим кривую, заданную параметрически (

):

Найдем явный вид:

.
Из параметрической формы видно, что
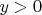
,

. Следовательно, мы имеем верхнюю полуокружность радиуса

с центром

.
Значение

соответствует точке

,

-- точке

,

-- точке

(предельные точки не принадлежат кривой).
Параметризация выбрана не случайно: она
естественная, т.е.

соответствует длине дуги (именно такой параметр подразумевается в уравнении геодезических). Проверим это. Найдем касательный вектор

.


Найдем его длину:

Единичность касательного вектора говорит о том, что параметр

естественный.
Раскроем абсолютный дифференциал в уравнении геодезических, получим

.
Вычислим это в компонентах, подставляя

(см. предыдущее сообщение) и

:

(остальные

равны нулю)


(остальные

равны нулю)

Итак,

, поэтому указанные в Википедии полуокружности на полуплоскости Пуанкаре действительно являются образами геодезических на плоскости Лобачевского.
Продолжение следует.



