Что ж, розъяснуйте откуда берутся условия 6.
Там же написано: "из общих принципов дифференциально-геометрического подхода к непрерывным симметриям геометрических объектов, определенных на гладком многообразии". И ссылка есть на книгу Дубровина, Новикова и Фоменко "Современная геометрия". Не знаю как вы, а я не силен в уравнениях Киллинга и в производных Ли. Если действительно интересно как получаются условия (6), могу адресовать к соавтору. На форум он вряд ли пойдет, но в личной переписке, надеюсь, ответит.
Я полагал, что язык современной геометрии и физики вам будет лучше понятен, чем "нечитаемые" изложения Гарасько. Что касается меня, то мне более понятен еще более архаичный язык Лаврентьева и Шабата, примененный в практически аналогичной ситуации для аналитических функций от двойных чисел:
http://hypercomplex.xpsweb.com/page.php?lang=ru&id=144 (стр.57)
Там рассматривается независимость производной функции гиперкомплексной переменной от направления, откуда и возникают для двойных чисел гиперболические условия Коши-Римана в виде двух уравнений "без минуса", как вы когда-то выражались. Для четверных чисел
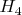
, условий типа гиперболических Коши-Римана для четырех скалярных функций существенно больше, все они "без минуса", а в качестве решений дают бесконечнопараметрическое множество четырех сопряженных скалярных функций, вместе задающих h-аналитическую функцию гиперкомплексной перменнной
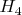
. С любой из так сконструированных функций связывается конкретное конформное преобразование плоского финслерова пространства, ассоциированного с алгеброй
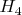
. Поскольку h-аналитических функций от
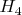
бесконечное множество, постольку и множество конформных преобразований четырехмерного пространства Бервальда-Моора так же бесконечно много.
В случае двумерия невидно как они воспроизводят обычные конформные преобразования
От системы уравнений, задающих условия Коши-Римана в четверных числах перейти к условиям для двойных - нет никаких проблем. Просто все лишние условия, кроме двух, исчезают.
которые кстати неабелевы и бесконечномерны.
На счет абелевости группы конформных преобразований четырехмерного пространства Бервальда-Моора, это мы с соавтором, похоже, погорячились. Впрочем, имелись ввиду только такие конформные преобразования, которые соответствуют растяжениям без трансляций. Тут, на сколько я понимаю, примерно такая же ситуация, как в случе с изометриями. В
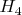
полная группа изометрических преобразований является неоднородной и неабелевой, а группа гиперболических поворотов - однородной и абелевой. В любом случае, на бесконечномерность группы конформных преобразований
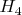
данный нюанс никак не влияет.
Можно перейти к резюме?
Вы по-прежнему считаете, что четырехмерное плоское финслерово пространство с метрической функцией Бервальда-Моора обладает конечномерной группой конформных преобразований?