Гравитация и двухмерный мир

[Renaldas]

Задался следующим вопросом, можно ли как-н привлечь математику и построить формулу "гравитационного воздействия" в двухмерном мире? По аналогии с трехмерной нашей формулой напрашивалось бы перемножить двухмерную "массу" тел (или произведение площади на плотность "вещества" в ней) и разделить это на какую-то степень расстояния (в трехмерном мире - это квадрат), введя коэффициент пропорциональности - G.

У кого-н есть идеи, или возможно физики/математики уже решили эту задачу?

[whiterussian]

это, без сомнений!, было уже сделано. И для двухмерия, и для ($3+n$)-мерия.

[Munin]

И для одномерия (1 пространственная координата + 1 временная), кажется, тоже.

О, пардон, вы об этом уже сказали, частный случай при $n=-2.$

[tola]

Если не секрет, а для чего такая экзотика, для чего это надо?

[Mega Sirius12]

будет тоже самое, только в двухмерии расстояние в знаменателе будет в единичной степени

[Renaldas]

whiterussian в сообщении #498046 писал(а):

это, без сомнений!, было уже сделано. И для двухмерия, и для ($3+n$)-мерия.

Не могли бы Вы написать общую формулу для эн-мерия?

[Joker_vD]

$$\vec F_{12}=G\frac{m_1m_2(\vec r_1-\vec r_2)}{\|\vec r_1-\vec r_2\|^3}.$$

Чем плохо? Благо, двумерного мира не существует. Здесь $F_{12}$ — сила, с которой первое тело действует на второе.

[whiterussian]

Joker_vD
Вы неправы.

В общем случае, гравитационная сила $F\sim \frac{1}{r^{D-1}}$, где $D$ - число измерений.

[Joker_vD]

whiterussian
А почему?

[whiterussian]

Joker_vD в сообщении #498196 писал(а):

А почему?

Извините, я не поняла вопроса. Почему что?

[arseniiv]

Почему так определяют силу, наверно. (Мне тоже интересно.)

[Munin]

tola в сообщении #498124 писал(а):

Если не секрет, а для чего такая экзотика, для чего это надо?

Просто обычные упражнения в теорфизике. Исследование "игрушечных" моделей, исследование свойств настоящих моделей - вдруг они неожиданно ответят на вопросы, которые мы и не задавали? Например, исследование закона Ньютона в $n$ измерениях дало интересный результат: устойчивые орбиты планет в многомерных пространствах невозможны. После этого на эту тему стали произноситься идеи типа антропного принципа.

Joker_vD в сообщении #498196 писал(а):

А почему?

arseniiv в сообщении #498203 писал(а):

Почему так определяют силу, наверно. (Мне тоже интересно.)

Потому что фундаментальным считается не закон для силы, а уравнение поля - в данном случае уравнение для гравитационного потенциала, уравнение Пуассона
$\Delta\varphi=4\pi G\rho,$
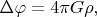
для которого закон Кулона (Ньютона) - всего лишь фундаментальное решение (функция Грина). Предполагается, что для $n$-мерного пространства уравнение Пуассона аналогично:
$\displaystyle\Bigl(\sum\dfrac{\partial^2}{\partial x_i^2}\Bigr)\varphi=4\pi G\rho.$

Но это обобщение ньютоновской теории на произвольные измерения, а я думал, речь об ОТО, а то и о квантах. Здесь whiterussian лучше просветит.

[Joker_vD]

А, точно, нам еще что-то такое на УМФ рассказывали... там еще площадь $n$-мерной сферы вроде встречалась... Но в любом случае, чем задание одного закона для несуществующей реальности хуже, чем задание другого?

[Утундрий]

Строго двумерная (не просто упрощениями сводящаяся к функциям двух переменных) гравитация - штука довольно скучная. Ибо (и я особенно подчёркиваю это ибо) для $n=2$ справедливо тождество $\[ R_{\mu \nu } - \frac{1} {2}Rg_{\mu \nu } \equiv 0 \] $.

[Munin]

Пардон, а коэффициент $-\tfrac{1}{2}$ в двух измерениях сохраняется? Вроде, он выводится из условия поперечности, и сам вычисляется из величины размерности пространства.

-- 01.11.2011 21:28:15 --

Joker_vD в сообщении #498225 писал(а):

Но в любом случае, чем задание одного закона для несуществующей реальности хуже, чем задание другого?

Ничем, просто другой закон меньше оснований называть "гравитацией" :-)

А насчёт несуществующей - с теорией струн, например, ещё вопрос.