В момент времени

система находиться в положении покоя, точка M находится в положении

.
Без начальной скорости точка скатывается по гладкой трубке. Соответственно куб, с длинной ребра

начинает раскручиваться в положительном направлении

.
Найти: относительные скорость и ускорение

и
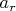
точки M в момент вылета из трубки, угловые скорость и ускорение

и

куба в тот же момент.
Масса куба

, масса мат. точки


Фиг. 1
Классика жанра, законы сохранения кинетического момента (не знаю почему физики говорят "сохранение момент импульса" а кафедра теомеха предпочитает сохранять "кинетический момент", ну да ладно).

- момент инерции куба.
Сохраняем кинетический момент:

Тут у нас

относительная скорость

,

- переносная скорость

где

- расстояние от оси до точки. Закон изменения этого расстояния достаточно жесток. Фиг. 2 и теорема косинусов дает такой вот результат:

Фиг. 2

Тогда вектор относительного импульса точки сначала проецируем на ось, перпендикулярную оси

, а потом умножаем на плечо:

Для переносной составляющей:

Итого

перепишем в виде:

Выражаем отсюда

:

Задача с двумя степенями свободы, можно и нужно записать еще одно уравнение:

Ключевой момент: как решить такую систему уравнений относительно

и

, или их производных, короче как нибудь. Строго говоря как вообще решить эту задачу?

(Оффтоп)
Пока набирал пришла мысль "взять и подставить второе в первое". Сейчас попробую, потом напишу что получилось, но, боюсь ничего хорошего не выйдет. И не выходит, диффур, даже не просто диффур, а "огого диффур!"



