Someone, попробовал, но не могу довести до конца. Предполагаю, что

является

-множеством, тогда

.
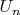
- произвольное открытое. Рассматриваю

.

можно представить в виде не более чем счётного объединения интервалов вида

,

представляется в виде не более чем счётного

, таких что

и т.д. Имеем систему вложенных интервалов:

. А что с ними делать дальше, не понимаю.