Ёж (метрическое пространство)

[maxmatem]

Слышал про такое метрическое пространство. Задана окружность единичного радиуса и точка $O$ -центр окружности. Расстояние измеряется следующим образом. Если две точки лежат на одном радиусе то расстояние такое $\rho(x;y)=\rho_{e}(x;y)$. Если точки лежат на разных радиусах то
$\rho(x;y)=\rho_{e}(x;O)+\rho_{e}(O;y)$, где $\rho_{e}(x;y)$-это евклидова метрика. Итак если окружность имеет один радиус , тогда все точки данного пространства находятся именно на этом радиусе и еж будем называть еж колючести один. Соответственно если окружность имеет $n$ радиусов и значит все точки ежа находятся на этих радиусах и он имеет $n$-колючесть.
Где про такое пространство можно почитать?
Самое пока что не ясное как доказать что ёж колючести 2 , изометричен числовому отрезку длины два со стандартной евклидовой метрикой

[ewert]

maxmatem в сообщении #486487 писал(а):

Самое пока что не ясное как доказать что ёж колючести 2 , изометричен числовому отрезку длины два со стандартной евклидовой метрикой

Развернуть эти два радиуса в один диаметр.

[alex1910]

Более употребительное название - французская железнодорожная метрика.

[Someone]

Далее следует совершенно не формальный текст.

Если $\tau$ - кардинал (конечный или бесконечный), то (метрический) ёж колючести $\tau$ строится так. Берём $\tau$ экземпляров отрезка $[0,1]$, склеиваем все точки $0$ в одну точку, а расстояние между точками определяем так: если точки лежат на одной игле, то расстояние между ними равно обычному расстоянию на отрезке, а если на разных - то сумме расстояний до $0$.

Часто рассматриваются также другие топологии на еже.
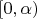
Компактная топология определяется так. Точки игл, отличные от $0$, в качестве окрестностей имеют обычные интервалы, а окрестность $0$ должна содержать все иглы, кроме конечного числа, а с этими пересекаться по множеству вида $[0,\alpha)$ (для разных игл $\alpha$ может быть разным; впрочем, можно ограничиться и одинаковыми, поскольку всегда можно взять меньшее из них).
Другие топологии такого рода получаются, если в последнем определении вместо конечного числа взять фиксированное бесконечное (не превосходящее $\tau$, естественно). Но здесь уже есть существенная разница, брать ли на всех иглах $\alpha$ одинаковым или разным.
Можно, наверное, придумать и другие топологии.

Мне помнится, что эти ежи употребляются, в основном, для построения контрпримеров, но и то не часто.
О метрическом еже есть интересная теорема: счётная степень метрического ежа колючести $\tau\geqslant\aleph_0$ является универсальным пространством в классе метризуемых пространств веса $\tau$ (то есть, каждое метризуемое пространство веса $\tau$ вкладывается в эту счётную степень).

alex1910 в сообщении #486517 писал(а):

Более употребительное название - французская железнодорожная метрика.

Кем "более употребительное"? Впервые такое слышу. Хотя о еже знаю уже больше 40 лет.

[AD]

maxmatem в сообщении #486487 писал(а):

Самое пока что не ясное как доказать что ёж колючести 2 , изометричен числовому отрезку длины два со стандартной евклидовой метрикой

Угадайте изометрию, она напрашивается

[alex1910]

Someone в сообщении #486519 писал(а):

Кем "более употребительное"? Впервые такое слышу. Хотя о еже знаю уже больше 40 лет.

Карта жел. дорог франции лет 100 назад выглядела, в основном, как лучи, выходящие из Парижа. Соотв. метрика - это кратчайший километраж от станции до станции по этой системе жд. А обобщения пошли уже потом.

[Someone]

Начхать на карту железных дорог Франции, тем более - столетней давности. Я такого названия метрики ежа за 40 лет ни разу не слышал.

[Padawan]

Someone в сообщении #486549 писал(а):

Начхать на карту железных дорог Франции, тем более - столетней давности. Я такого названия метрики ежа за 40 лет ни разу не слышал.

Да. Я когда про эту железную дорогу в википедии прочитал, тоже удивился Ёж.

[ИСН]

А мне железнодорожная аналогия показалась вполне естественной, только применительно к России.

[alex1910]

Someone в сообщении #486549 писал(а):

Начхать на карту железных дорог Франции, тем более - столетней давности. Я такого названия метрики ежа за 40 лет ни разу не слышал.

1. Не надо чихать на антиквариат.
2. Любая общая теория выросла из какой-то конкретной задачи.

[Joker_vD]

maxmatem в сообщении #486487 писал(а):

Самое пока что не ясное как доказать что ёж колючести 2 , изометричен числовому отрезку длины два со стандартной евклидовой метрикой

Нарисуйте единичную окружность и проведите в ней диаметр, ну и... "Смотри!" (с) древние индусы