К. Куратовский, А. Мостовский- Теория множеств. Она что, плохая?
Не знаю, я её не читал. Во всяком случае, термин "независимые множества" -- весьма экстравагантен. Поскольку он жёстко закреплён за теорией вероятностей (и там независимость событий вовсе не сводится к "независимости" множеств в смысле Куратовского-Мостовского: независимость событий -- требование, в принципе, гораздо более жёсткое, но изредка и чуть-чуть более слабое). И уж называть точки или там векторы "последовательностями" -- совсем неприлично.
Ну очевидно, что любое такое пересечение не пусто, т.к. оно описывается вполне явно. Принадлежность точки пересечению сводится к выполнению системы неравенств, каждое из которых накладывается на только одну из координат. Поэтому любым таким пересечением будет
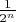
-ая часть от от полного кубика, для которой какие-то из координат принадлежат левой половине едничного отрезка, а все остальные -- правой.
Нечаянно эти события окажутся независимыми и в нормальном, человеческом, теоретико-вероятностном смысле, и это тоже тривиально (естественно, в предположении равнномерности распределения).



