Если

-- векторное пространство над полем

, то линейное отображение

этого пространства в своё второе сопряженное, задаваемое формулой

,

,

является иньективным. Это равносильно тому, что для любого

, существует

, такое, что
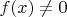
. Последнее, в свою очередь, следует из того, что

можно дополнить до базиса.
Пусть теперь

-- модуль над кольцом

. Будет ли аналогичное отображение

инъективным в общем случае? Другими словами, следует ли из того, что

существование

такого, что
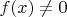
.
Если нет, то какие для этого достаточные условия. Например, если

- тело, то будет. А если целостное кольцо с единицей?



