IMC 2011 problems

[myra_panama]

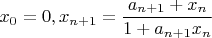
(*).Let $(a_n)\subset (\frac{1}{2},1)$. Define the sequence $x_0=0,\displaystyle x_{n+1}=\frac{a_{n+1}+x_n}{1+a_{n+1}x_n}$. Is this sequence convergent? If yes find the limit.

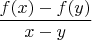
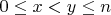
(**).Let $f$ be a polynomial with real coefficients of degree $n$. Suppose that $\displaystyle \frac{f(x)-f(y)}{x-y}$ is an integer for all $0 \leq x<y \leq n$. Prove that $a-b | f(a)-f(b)$ for all distinct integers $a,b$.

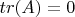
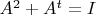
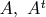
(***).Does there exist a real $3\times 3$ matrix $A$ such that $tr(A)=0$ and $A^2+A^t=I$? (tr(A) denotes the trace of $A,\ A^t $ the transpose of $A$, and $I$ is the identity matrix.)

(****). Let $p$ be a prime number. Call a positive integer $n$ interesting if

$$x^n-1=(x^p-x+1)f(x)+pg(x)$$

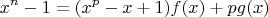
for some polynomials f and g with integer coefficients.
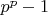
a) Prove that the number $p^p-1$ is interesting.
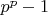
b) For which $p$ is $p^p-1$ the minimal interesting number?

[nnosipov]

(****), a), b) Hint: the polynomial $x^p-x+1$ is irreducible over $\mathbb{F}_p$.

[myra_panama]

Yes.Since $x^p-x+1$ is irreductibe in $F_p[X]$ then $F_p[X] / (x^p-x+1)$ is a field , with order $p^p$

[Sonic86]

myra_panama в сообщении #473086 писал(а):

*).Let $(a_n)\subset (\frac{1}{2},1)$. Define the sequence $x_0=0,\displaystyle x_{n+1}=\frac{a_{n+1}+x_n}{1+a_{n+1}x_n}$. Is this sequence convergent? If yes find the limit.

Положим $x_n = \th \alpha _n, a_n = \th \beta _n$. Поскольку
$\th (a+b) = \frac{\th a + \th b}{1 + \th a \th b}$ и $0<A \leqslant \beta _n < + \infty$, то $x_n = \th (\alpha _0 + \sum\limits_{k=0}^{n-1} \beta _k) \to 1$ при $n \to + \infty$. (получается, нижнее ограничение на $a_n$ енсущественно, лишь бы положительно, а верхнее - точно)