(*).Let
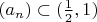
. Define the sequence
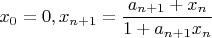
. Is this sequence convergent? If yes find the limit.
(**).Let

be a polynomial with real coefficients of degree

. Suppose that
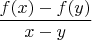
is an integer for all
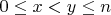
. Prove that
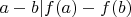
for all distinct integers

.
(***).Does there exist a real

matrix

such that
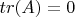
and
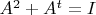
? (tr(A) denotes the trace of
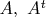
the transpose of

, and

is the identity matrix.)
(****). Let

be a prime number. Call a positive integer

interesting if
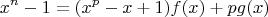
for some polynomials f and g with integer coefficients.
a) Prove that the number
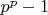
is interesting.
b) For which

is
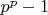
the minimal interesting number?