Кубический корень - многозначная функция, т.е., если формально, то
![$\sqrt[3]x$ $\sqrt[3]x$](https://dxdy-03.korotkov.co.uk/f/a/7/f/a7f514b4cf7be7d42b724cd014fd711382.png)
- не число, а множество, вообще говоря (а именно, при

), из 3 элементов. Например,
![$\sqrt[3]{-8}=\{-2;1\pm i\sqrt3\}$ $\sqrt[3]{-8}=\{-2;1\pm i\sqrt3\}$](https://dxdy-02.korotkov.co.uk/f/9/6/5/9655016c56886d2c15a2446d124fac2582.png)
.
Поэтому правильнее говорить не о кубическом корне из числа

, а об одном из значений кубического корня из

.
Это если мы работаем с комплексными числами. Если же ограничиться только действительными числами, то:
1) Есть понятие арифметического кубического корня. Он определен только при

и определяется как решение

уравнения

.
2) Поскольку

- нечетное число, то можно определить корень кубический из произвольного действительного числа

как решение
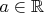
уравнения

.
Но пользоваться этими понятиями кубического корня можно, только если мы работаем исключительно в поле действительных чисел. Если в промежуточных выкладках мы используем комплексные числа, то использование этих понятий незаконно и может привести к противоречиям.



