Решил изложить элементарное (и подробное) доказательство, причем в том виде и в тех обозначениях, в каком оно было когда-то получено.
Доказываем утверждение:
На сторонах заданного единичного квадрата и их продолжениях не существует точек, расстояния от которых до каждой из вершин квадрата выражаются рациональными числами.
Доказательство. Предположим противное и хотя бы одна такая точка существует. Пусть

- расстояние от этой точки до ближайшей из верщин квадрата, лежащей на той же стороне квадрата, что и искомая точка,
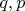
- натуральные взаимно простые числа

. Очевидно, что

удовлетворяют одной из двух систем уравнений:


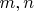
- целые числа. Причем первой системе

,

удовлетворяют, когда искомая точка лежит между вершинами квадрата
и при этом

, второй системе

,

удовлетворяют, когда точка лежит на продолжении стороны квадрата. В обоих случаях

,
поскольку для второй системы

, а для первой

>

. Отрезки длиной

являются в обеих случаях целочисленными
сторонами треугольника с площадью равной

. В обоих случаях очевидно, что

,

. Кроме того,

- четно,

- нечетно. Действительно, в противном случае имеем противоречие:

. Легко вычислить, что для первой и второй систем

удовлетворяет уравнению

Докажем следующее утверждение: если натуральные числа

удовлетворяют уравнению

, то в случае

существует натуральное

такое, что

удовлетворяют

, в случае

существует натуральное

такое, что

удовлетворяют

, причем в обоих случаях

. Действительно, уравнение

, произведя
перегруппировку слагаемых, можно записать в следующем виде:

Каждый из сомножителей в левой части

положителен, поскольку если среди них есть отрицательные, то в нашем случае это может
быть только один из них, но тогда произведение всех сомножителей меньше

, что противоречит

. Значит, все сомножители
положительны и поэтому

и отрезки с длинами

образуют треугольник с целочисленными
сторонами и площадью в соответствие с формулой Герона равной

.
Следовательно, высота, опущенная на сторону длины

, очевидно, имеет длину

и

. Длину отрезка от основания этой
высоты до ближайшего конца стороны треугольника длиной

обозначим

. Величины

очевидно, удовлетворяют либо

, когда основание высоты лежит на стороне треугольника и в этом случае

, либо

, когда основание высоты лежит на
продолжении стороны треугольника и в этом случае

. Остается показать, что

- натуральное число. Из первого уравнения

или

следует, что

- натуральное число, вычитая первое уравнение из второго получаем:

т.е.

- рациональное число. Из того, что

-натуральное, а

- рациональное следует, что

- число натуральное. Утверждение
доказано.Из всех натуральных чисел

, для которых уравнение

разрешимо в натуральных числах выберем наименьшее. Разберем два случая:
1.Наименьшее

удовлетворяет

Тогда для первого уравнения существуют

четное, такие, что

,

,

. Для второго уравнения существуют

четное,
такие, что

,

,

. Величины

связаны соотношениями

,

Положим

,

,

,

. Тогда

,

,

,

, это следует из того, что если

делится на

и

то

Все

,

попарно взаимно просты, поскольку если

, то

Подставляя

в соотношения

получим:


Из

следует, что

. Далее, среди

есть обязательно только одно четное число, остальные нечетные. Это
следует из четности

и взаимной простоты

. Четное число либо

либо

. Действительно, пусть это
не так. Тогда

,

и левая часть

на

не делится, правая же часть

, очевидно, на

делится. Полученное
противоречие доказывает утверждение о четности

или

. Следующие утверждения легко следуют из взаимной простоты

. А именно:

,

. Из этих утверждений, а также из того, что

четное число и из

следует:


Рассмотрим следующее уравнение для определения

:

Это уравнение идентично уравнению

для определения

.
Справедливо следующее утверждение. Уравнение

имеет корень

, являющийся четным натуральным числом и

. (Метод спуска)
Из уравнения

имеем:

Принимая во внимание

и


Обозначим

,

.

и

- целые, четные положительные числа.
Действительно, из

следует, что

и

Следовательно, оба числа

больше

. А поскольку, как было показано выше

и

- числа нечетные,

- число
четное и, следовательно,

четные числа.

удовлетворяют системе уравнений:



следует из определения

, а

следует из

и формулы умножения корней для

.
Обозначим

и

,

,

. Из четности

следует четность

.
Уравнения

,

в новых обозначениях перепишутся так:


Покажем, что

и

числа разной четности. Предположим противное:

и

оба нечетные числа. Пусть

,

. Поскольку левая часть

в силу четности

делится
на

, а правая часть

делится только на

в силу нечетности

, то

т.е.

. Но тогда
левая часть

делится только на

, а правая часть

в силу четности

или

делится по крайней мере на

.
Полученное противоречие доказывает, что

числа разной четности и, следовательно,

- число нечетное. Из нечетности

и

следует, что

.
Покажем теперь, что

. Предположим
противное,

. Тогда существует нечетное простое число

такое, что

,

,

. Подставляя
эти выражения в

получим выражение для

. А именно:

. Таким образом

делится на

. А поскольку

простое число, то на

делится

и, следовательно

и

не взаимно
просты. Полученное противоречие доказывает, что

.
Аналогично доказывается, что

.
Уравнение

запишем так:

. Правая
часть его делится на

. Но поскольку

на

не делится, то на

должно делиться

. А это
возможно,только если

. Итак, доказано, что

и уравнение

запишется так:

.
Деля обе части на

, считая, например,

четным числом и полагая

получаем уравнение

.
Поскольку

и

взаимно просты, а

- простое число, одно из чисел

,

полный квадрат, а другое - полный квадрат, умноженный на

.
Например,

,

. Квадраты корней уравнения


,

. Подставляя в эти выражения значения

,

,

получаем, что

и

. Таким образом, корень уравнения


- четное натуральное
число. Покажем, что

. Действительно,

,

,

.
Полученное противоречие , а именно

, доказывает случай

.
2.Наименьшее

удовлетворяет

.
Рассматривается аналогично предыдущему "Наименьшее

удовлетворяет

". Отличия заключаются в следующем:
Уравнение

меняется на

Уравнение

меняется на

, откуда

Уравнение

меняется на

Уравнение

меняется на

Уравнение

меняется на

Остается верным неравенство

. Действительно,

.Отсюда следует

и

. Далее доказательство точно следует схеме доказательства предыдущего случая, т.е. доказывается существования натурального корня у измененного уравнения

, четного и меньшего

.