Помогите пожалуйста проверить рассуждения.
Цитата:
Покажите, что отображение
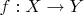
сюръективно, если и только если для любого множества

справедливо
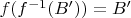
Мои рассуждения:
из

- сюръекция
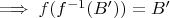
.
Т.к.

- сюръекция, то

, что
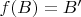
Пусть
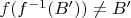
, пусть
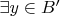
такой, что
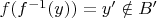
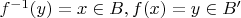
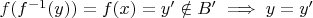
, чего не может быть, следовательно таких

не существует и следовательно
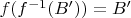
.
В обратную сторону, из
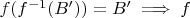
- сюръекция.
Пусть это не так, т.е.
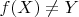
. Пусть
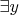
такое, что
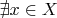
, что
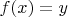
. Из таких

составим

, тогда
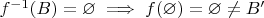
, что есть противоречие, следовательно

- сюръекция.
Цитата:
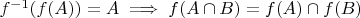
для любой пары

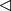
Пусть это не так, пусть
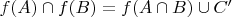
, причём
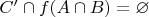
.
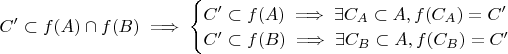
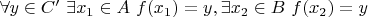
,
при этом
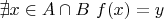
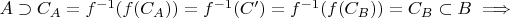
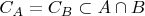
,
но
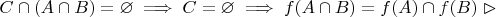
Должен ли я здесь ещё проверить предположение, что
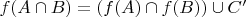
?



