Возможно ли неравенство

[RIP]

nnosipov в сообщении #458074 писал(а):

Есть какая-то новизна в подобных задачах?

Не знаю. Подход расскажите (небось, какой-нибудь метод спуска?).
$4a+1$, наверно, можно увеличить, но тут уже совсем тривиально не получается, надо думать.

[nnosipov]

Расскажу обязательно, хотя что тут может быть, кроме спуска. Самому надо понять, можно ли увеличить. Но вот завтра у меня экзамены начинаются, и это удовольствие на три дня ...

[nnosipov]

Итак, приступим. Рассматриваем уравнение вида

$$ x^2-Ay^2=B. \eqno(*) $$

Пусть $\varepsilon=x_0+y_0\sqrt{A}>1$ --- наименьшее решение ассоциированного уравнения Пелля $x^2-Ay^2=1$.
Теорема. Базовые решения $\alpha=X+Y\sqrt{A}$ уравнения $(*)$ определяются условиями:

$$ \frac{\sqrt{B}}{2\sqrt{A}} \,(\varepsilon^{-1/2}-\varepsilon^{1/2}) \leqslant Y< \frac{\sqrt{B}}{2\sqrt{A}} \,(\varepsilon^{1/2}-\varepsilon^{-1/2}), \quad X=\sqrt{AY^2+B} $$

в случае $B>0$; если же $B<0$, то

$$ \frac{\sqrt{|B|}}{\sqrt{A}} \leqslant Y<\frac{\sqrt{|B|}}{2\sqrt{A}} \,(\varepsilon^{1/2}+\varepsilon^{-1/2}), \quad X=\pm \sqrt{AY^2+B}, $$

а также

$$ Y=\frac{\sqrt{|B|}}{2\sqrt{A}}\,(\varepsilon^{1/2}+\varepsilon^{-1/2}), \quad X=-\sqrt{AY^2+B}. $$

Базовость означает, что $\alpha \in [q,q\varepsilon)$, где $q=\sqrt{|B|/\varepsilon}$ (обычно берут $q=1$, но при указанном значении $q$ интервал для $Y$ получается самым узким). Произвольное решение уравнения $(*)$ представляется в виде $\pm \alpha_j\varepsilon^k$, где $k \in \mathbb{Z}$, а $\alpha_j$ --- одно из базовых. В качестве примера решим уравнение

$$ x^2-(d^2-1)y^2=B, $$

где $|B|<Cd$ ($d$ произвольно, $C$ фиксировано). Имеем $\varepsilon=d+\sqrt{d^2+1} \asymp d$, поэтому для $Y$ имеем оценку $|Y|<C_1$, где $C_1$ не зависит от $d$ и $B$ (но зависит от $C$). Фиксируем одно из таких $Y$. Тогда для $X^2=d^2Y^2+Y^2+B$ имеем $(d|Y|-C_2)^2<X^2<(d|Y|+C_2)^2$, где $C_2$ зависит только от $C$. Значит, $X^2=(d|Y|+k)^2$, где $|k|<C_2$. Подставляем это в уравнение и получаем

$$ B=2k|Y|d+k^2-Y^2. \eqno(**) $$

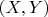
Таким образом, имеется конечное число линейных (относительно $d$) выражений для $B$. Оставим из них те, для которых $|B|<Cd$ при всех достаточно больших $d$ (нижняя граница для $d$ зависит только от $C$; маленькие $d$ разбираем отдельно). Для каждого из оставшихся выражений $(**)$ находим все базовые решения $(X,Y)$ (в роли $Y$ --- константы $<C_1$, в роли $X$ --- линейные выражения относительно $d$) и пишем ответ. (Небрежность в оценках здесь есть, так что проверяйте.)

Теперь наша задача (вот тут я старался быть аккуратным). Она сводится к исследованию уравнения

$$ x^2-(d^2-4)y^2=B, $$

где $d=2a+1$, $x=b$, $y=c$, при этом $-4a+3<B<-2a+2$. Здесь

$$ \varepsilon=\frac{d(d^2-3)}{2}+\frac{d^2-1}{2}\sqrt{d^2-4} =4a^3+6a^2-1+2(a^2+a)\sqrt{(2a-1)(2a+3)}. $$

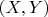
При ограничениях на $B$ из теоремы можно вывести для базовых решений $(X,Y)$ двойное неравенство

$$ 1 \leqslant Y<\sqrt{2}a. $$

Но тогда для $X^2=((2a+1)^2-4)Y^2+B$ с учётом ограничений на $B$ мы получили бы

$$ ((2a+1)Y-2)^2<X^2<((2a+1)Y)^2, $$

откуда $X^2=((2a+1)Y-1)^2$ и, как следствие, уравнение

$$ 4Y^2-2(2a+1)Y+1-B=0. $$

Дискриминант этого уравнения должен быть точным квадратом:

$$ 4a^2+4a-3+4B=Z^2. $$

Вновь учитывая ограничения на $B$, приходим к неравенствам

$$ (2a-3)^2<Z^2<(2a+1)^2. $$

Значит, $Z^2=(2a-1)^2$ и $B=-2a+1$. Таким образом,

$$ Y=a=\frac{\sqrt{2a-1}}{2\sqrt{(2a-1)(2a+3)}}\, (\varepsilon^{1/2}+\varepsilon^{-1/2}), \quad X=-2a^2-a+1. $$

Все искомые пары $(c,b)$ натуральных чисел теперь можно найти из формулы

$$ c+b\sqrt{(2a-1)(2a+3)}=(-2a^2-a+1+a\sqrt{(2a-1)(2a+3)})\,\varepsilon^k =(2a^2+a-1+a\sqrt{(2a-1)(2a+3)})\,\varepsilon^{k-1}, $$

где $k=1,\,2,\,\ldots$ (и, конечно, $a>1$ --- произвольно).

Не вижу, почему бы всё это не прошло и для других интервалов для $B$.

[nnosipov]

Если переходить к совсем конкретным примерам, то вот типичная картина: если $d$ достаточно велико и $-12d<B:=x^2-(d^2-1)y^2<0$, то

$$ B \in \{-12d+13,-12d+37,-10d+26,-8d+8,-8d+17,-6d+10,-4d+5,-2d+2\}. $$

(Здесь можно считать $d \geqslant 25$.)

[nnosipov]

Для RIP: вот Вы и появились, прошу полюбопытствовать.

[RIP]

Да я уже давно появился и полюбопытствовал. Я здесь частенько бываю, просто обычно ничего не пишу (да и просматриваю по диагонали), ибо некогда.

[nnosipov]

Ну что же, тогда ладно. (У меня в тексте выше есть какие-то опечатки, не успел поправить, но это мелочи.)

[arqady]

(Оффтоп)

RIP в сообщении #460676 писал(а):

Я здесь частенько бываю, просто обычно ничего не пишу (да и просматриваю по диагонали), ибо некогда.

У меня всё вточности то же самое!

[nnosipov]

arqady в сообщении #461411 писал(а):

(Оффтоп)

RIP в сообщении #460676 писал(а):

Я здесь частенько бываю, просто обычно ничего не пишу (да и просматриваю по диагонали), ибо некогда.

У меня всё вточности то же самое!

(Оффтоп)

Да уж, дел у нас у всех хватает, тут ничего не попишешь. И вообще, в отпуск уже пора