Дробная и действительнозначная итерация функции

[arseniiv]

Помните вопрос про дробную производную? Ещё мне не давала покоя итерация.
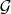
Можно ли найти оператор $\mathcal G$, действующий на каком-нибудь довольно большом множестве функций такой, что $\mathcal G f^{[n]} = n \mathcal G f$? ($f^{[n]} = \underbrace{f \circ\ldots\circ f}_n$, ну и отрицательные через обратную, если она существует, а $f^{[0]} = \operatorname{id}$.) Тогда если найдётся ещё и $\mathcal G^{-1}$, можно будет определить вообще действительнозначную итерацию. Только, кажется, даже для многочленов уже такой оператор не найти (или только кажется?). А вот для степенных функций легко получается определить нецелую итерацию: $\left( x^a \right)^{[s]} = x^{a^s}$. 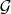Только $\mathcal G$ не придумывается. Двойное логарифмирование к другому результату приводит. Хотя можно какой-нибудь обобщённый $\tilde{\mathcal G}\colon \tilde{\mathcal G} f^{[n]} = \xi(\tilde{\mathcal G} f, n)$, тогда оно пойдёт.

-- Ср июн 08, 2011 23:55:08 --

Нет, двойное логарифмирование не идёт.

[arseniiv]

Кажется, я неправильный оператор написал. В общем, щас посмотрю, что делают преобразования Фурье и Лапласа с производной, и вернусь.

-- Чт июн 09, 2011 01:20:46 --

В общем, как-то так пусть будет: $\mathcal G f^{[n]}(x) = \xi(\mathcal G f(x), x, n)$, хотя можно пытаться искать частный случай $\mathcal G f^{[n]}(x) = \xi(x)^n \mathcal G f(x)$.

[ИСН]

Я в детстве как-то для дробно-линейных функций вывел вторую, третью степень, угадал общую формулу, доказал по индукции, потом как-то обратил, совместил, получил таким макаром общую формулу для рациональных степеней, потом естественным образом обобщил по непрерывности на действительные.
Про фишку с матрицами узнал где-то через год.

[arseniiv]

А что с матрицами? Правильно понимаю, что что-то вроде такого?:
$\left[\begin{matrix} f(x) \\ \text{что-то} \end{matrix}\right] = \left[\begin{matrix} a & b \\ c & d \end{matrix}\right] \cdot \left[\begin{matrix} x \\ \text{что-то} \end{matrix}\right]$

[Kallikanzarid]

Рассмотрите сначала квадратный корень из матрицы вида

$$\begin{bmatrix}x & y \\ -y & x\end{bmatrix}.$$

[ИСН]

arseniiv в сообщении #456664 писал(а):

А что с матрицами?

Итерировать функции $ax+b\over cx+d$ - это всё равно что множить матрицы $\left(\begin{matrix} a & b \\ c & d \end{matrix}\right)$