По первому пункту. Второй случай тривиален, а для первого докажите, что именно так себя ведёт

(интеграл по оставшемуся участку даст в пределе ноль, т.к. там подынтегральная функция убывает более-менее экспоненциально). Для этого перейдите к экспоненте под интегралом, оцените логарифм в показателе по Тейлору и сделайте замену

.
Для второго примера: функция или очень монотонна (очень в том смысле что её производная отделена от нуля), или имеет внутри промежутка или на его конце локальный максимум, в котором первая производная равна нулю. В первом случае утверждение доказывается примерно как в предыдущем примере (из условий задачи следует, что максимальное значение функции в точности равно единице, иначе эти условия не могут быть выполнены). Во втором -- докажите, что этот предел не может быть конечным (он уходит на бесконечность со скоростью не менее
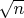
).
Только два замечания. Во-первых, Вы явно потеряли во втором примере

перед интегралом; найдите его. Во-вторых, условий на вторую производную там как-то явно недостаточно; надо бы дополнительно потребовать от второй производной если и не непрерывности, то хотя бы ограниченности.



