Если у Вас "вложение", то индуцированная топология совпадает с той, которая была
Выходит, при вложении
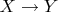
объект

становится (если сможет) подмножеством

? Например, когда множество рациональных чисел вкладывается в множество действительных чисел, становясь его подмножеством? Скажите, пожалуйста, как правильно назвать операцию отображения одного топологического пространства на другое, при котором возникает новое пространство с новыми топологическими свойствами? ("вложение" получается многозначным термином : когда вкладываешь силы в ребёнка, то он меняется ...).
-- Пн окт 18, 2010 09:20:06 --Fagot в сообщении #362221 писал(а):
Дыра - это замыкание компактного подмножества

в многообразии

.
Пусть

-- это точка в

... тут "дыра" -- это точка в

После некоторых размышлений данный результат показался не совсем абсурдным : топология имеет дело с непрерывностью и близостью, в этом смысле точка, что на множестве мощности континуума, что на дискретном множестве является, если подходить строго, как принадлежащей данному пространству. так и не принадлежащей ему (дырой) - "есть = ничему" ...



