Препод говорит, что автомат Мура выдаёт выходной сигнал ещё до момента, как поступил первый входной. Мне кажется, что это противоречит с определением автомата Мура, который этот же препод нам давал. Скажите, что сделать: определение подправить или не верить преподу по поводу лишнего выходного сигнала?
Вот определения из моих лекций.
Конечным дискретным автоматом называется кортеж

,
где

- входной алфавит,

- выходной,

- состояния,



- начальное состояние.
Абстрактный автомат в момент времени

находится в состоянии

. Находясь в момент времени

в состоянии

автомат:
(1) воспринимает входной сигнал

,
(2) выдаёт выходной сигнал

,
(3) переходит в состояние

.
Автомат Мили. Автомат Мура.
Автомат Мура.
Конец цитаты.
Но Когда дело доходит до построения автомата Мура, эквивалентного данному автомату Мили, или наоборот, то возникают проблемы с тем, что у Мура в начале работы есть лишний выходной сигнал, и вообще на равные входные последовательности эти автоматы выдают выходные последовательности разной длины (у Мура длиньше на единицу). Это что за эквивалентность такая, так сказать, с оговорками

.
Во вторых, при минимизации автомата Мура с помощью алгоритма Ауфенкампа-Хона (метод последовательных разбиений), препод заставляет делать первое разбиение с учетом как раз того лишнего выходного сигнала, о факте существования которого он утверждает.
Вот, почему мне не нравится позиция препода. Лишний сигнал - источник лишних проблем. В то время, как без него всё хорошо.
А противоречие в следующем. По данному определению

вообще неопределено для обоих автоматов. Если, скажем,

, то
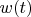
определено только начиная с

, так как определяется через

.
Что ещё хотел попросить... Препод, если дело касается определений, ссылается на "а в книжке написано...". Поэтому, мне хотелось бы знать не только ответ, но и ему можно найти подтверждение.
Простите за отсутствие лаконичности

.



