Как в школе правильно обозначать вектор?

[Someone]

Sashamandra писал(а):

А есть ли в самом тексте П.С.Александрова свидетельства, которые бы могли прояснить его собственное понимание выражения (x,y), другими словами, сузить круг интерпретаций?

Поищите сами. Если хорошо поищете - найдёте. Тем более, текст у Вас есть.

[Brukvalub]

Простите, что вмешиваюсь, но, как мне кажется, в понимании текста П.С.Александрова очень важно учитывать, что во-первых, вектор является формообразующим объектом в теории категорий для категории Vekt векторных пространств с морфизмами - линейными отображениями таких объектов, а, во-вторых, вектор является одним из простейших примеров тензора, а именно, тензором ранга (1,0) со всеми присущими тензорам особенностями. Без учета всех этих факторов понимание текстов по аналитической геометрии явно будет страдать однобокостью и останется поверхностным.

[Sashamandra]

Первое выражение, в котором используются фигурные скобки для обозначения векторов, я нашел на странице 21. Вот что там написано:

${\mathbf{u}} = x_1 {\mathbf{e}}_1 + x_2 {\mathbf{e}}_2 $ (3)
...
Равенство (3) часто записывается в виде

\[ {\mathbf{u}} = \{ x_1 ,x_2 \} \]

Из сопоставления двух формул я делаю выводы: 1) выражение {x,y} используется самостоятельно; 2) оно само обозначат вектор. А отсюда следуют все выводы, которые я перечислил выше для обозначения точки: {_,_} – функциональный символ от двух переменных со значениями в множестве векторов. Или я неправ?

[Brukvalub]

Конечно, но необходимо дополнительно учитывать все факторы, изложенные мной выше.

[Sashamandra]

Brukvalub писал(а):

Конечно

Конечно, неправ?

[Brukvalub]

Я писал не так.

[Sashamandra]

Ладно, проехали...

[Someone]

Sashamandra писал(а):

Из сопоставления двух формул я делаю выводы: 1) выражение {x,y} используется самостоятельно; 2) оно само обозначат вектор. А отсюда следуют все выводы, которые я перечислил выше для обозначения точки: {_,_} – функциональный символ от двух переменных со значениями в множестве векторов. Или я неправ?

Нет, не согласен. Там ещё какой-то базис подразумевается, так что значение этого функционального символа зависит от базиса, и обозначение нужно существенно усложнить. А с точками ещё сложнее, там и базиса мало, ещё опорная точка нужна (начало системы координат). Так что Вы не совсем правы. Займитесь этим.

А Вы не забыли, что там на самом деле подразумевается не векторное, а аффинное пространство? Так что вектор - это скорее класс эквивалентности упорядоченных пар точек $(M_1,M_2)$. Поэтому ещё надо выяснить, как со всем этим сообразуется запись вектора в виде $\overline{M_1M_2}$. Что Вы там накопали у П.С.Александрова по этому поводу?

А у Д.В.Клетеника $M(x,y)$ - это результат подстановки имени точки и имён её координат в трёхместный предикат? И опять там система координат где-то прячется... Спрашивается, как же это классики позволяют себе такие неточности?

[Sashamandra]

Someone писал(а):

Нет, не согласен. Там ещё какой-то базис подразумевается, так что значение этого функционального символа зависит от базиса, и обозначение нужно существенно усложнить.

А я вижу из Ваших слов, что Вы со мной согласились.

Конечно, рассматриваемый нами функциональный символ должен зависеть от выбранного базиса (и от выбранного пространства), но если эта зависимость не указывается явно, это не значит, что она отрицается. Ведь это обычное дело в математике — не выписывать зависимость от того, что в данном контексте считается заданным и неизменным. Мой тезис сводится лишь к тому, что круглые и фигурные скобки здесь (у П.С.Александрова) следует понимать как функциональные символы подобно тому, как в теории множеств фигурные скобки могут использоваться для обозначения функционального символа неупорядоченной пары, а круглые (или угловые) скобки — для упорядоченной пары.

Последние Ваши два абзаца опять-таки не затрагивают защищаемый мной тезис. Поэтому если Вы согласитесь со мной в обсуждаемом вопросе, то затем можно будет перейти и к затронутым Вами вопросам.

Добавлено спустя 25 минут 50 секунд:

Someone писал(а):

А у Д.В.Клетеника - это результат подстановки имени точки и имён её координат в трёхместный предикат?

Что касается Д.В.Клетеника, то у него имеется досадная ошибка, только непонятно, это ошибка в русском языке или в математике. На странице 5 уважаемый автор пишет:

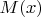
В дальнейшем символ $M(x)$ означает, что точка $M$ имеет координату $x$. Если $M_1 (x_1 )$ и $M_2 (x_2 )$ — две произвольные точки прямой...

Правильно следует читать этот текст так

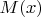
В дальнейшем выражение (терм) $M(x)$ означает точку $M$, имеющую координату $x$. Если $M(x_1 )$ и $M(x_2 )$ — две произвольные точки прямой...