Пример из первого параграфа второй главы. Рассмотрим высказывание

Это высказывание формализация следующих высказываний: Все люди – животные. Следовательно, голова человека есть голова животного. При этом,
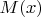
- «

есть человек»,

- «

есть животное», «

- голова

».

- функциональная буква с одним аргументом.
А теперь, имея в виду формализацией какого высказывания является эта формула, выберем область интерпретации

Первое, что приходит в голову, множество зверей (включая человека), но приглядевшись мы видим, что

- функциональная буква с одним аргументом, и следовательно ей должна быть сопоставлена функция из

в

Но

- голова

Итак, множество

должно состоять из животных и их голов. Развивая успех (или казус), теперь можно рассмотреть «голову головы» и т. д. Я наврал где-нибудь или так тому и быть?



