Joker_vDВозможно, следующее рассуждение чуть прояснит ситуацию, почему случай натуральных чисел хуже, чем отрезок
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
:
Возьмём какое-нибудь дискретное (т.е. между любыми двумя точками расстояние положительно) подмножество вещественной оси, обозначим его

(к слову сказать, поскольку вещественная прямая со стондартной метрикой сепарабельна, то

не более чем счётно). Определим

-алгебру подмножеств

как множество всех подмножеств, и на ней каким-то образом задим вероятность

. Возьмём и продолжим эту вероятность на все борелевские подмножества

- определим вероятность какого-нибудь подмножества в

, как вероятность пересечения этого множества с

. Понятно, что продолжение тоже останется вероятностью.
Теперь рассмотрим функцию распределения этой вероятности, т.е. функцию

. Функцию

, по теореме Лебега, можно разложить на 3 составляющие

, где

, функция

абсолютно непрерывна,

дискретна, а
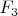
сингулярна (т.е. непрерывна и производная равна 0 почти всюду). Воспользовавшись дискретностью

, как подмножества

, совсем просто установить, что абсолютно непрерывная составляющая функции распределения равна нулю. Ваше требования на то, что все элементарные исходы равновозможны, обнуляет и дискретную составляющую (если, конечно, множество

бесконечно). В итоге

, т.е. функция распределения такой вероятностной меры обязана быть сингулярной.
Если рассматривать вероятность, "равномерно распределённую на отрезке
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
", то её функция распределения будет абсолютно непрерывна, чего в дискретном случае никак быть не может. "Виновата" в этом, отчасти, каноническая топология вещественной оси.



