
- 7 штук попарно антикоммутирующих, вещественных

матриц:

Обозначим
![$\gamma^{\mu\nu\lambda}=\frac{1}{3!}\gamma^{[\mu}\gamma^\nu\gamma^{\lambda]}$ $\gamma^{\mu\nu\lambda}=\frac{1}{3!}\gamma^{[\mu}\gamma^\nu\gamma^{\lambda]}$](https://dxdy-01.korotkov.co.uk/f/c/7/2/c723316de06ba8850b8401028228a5da82.png)
([] означает антисимметризацию).
Тогда величины

определяются с помощью столбца из

-и элементов

следующим образом:

,
где

-произвольные константы. Везде по повторяющемуся индексу подразумевается суммирование. (Греческие индексы пробегают значения от 1 до 7, тогда как латинские от 1 до 8).
Итак, для величин

получаем следующую систему уравнений:

которую прошу помочь разрешить.
Заметил, что если умножить это уравнение на

и просуммировать по

то первое слогаемое выпадает и остается:

Еще(уже с помощью компьютера) заметил, что если зафиксировать индекс

в

и рассматривать эти величины как
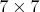
матрицу, то ее ранг равен 4. Этого я никак не могу доказать.
(Оффтоп)
Если нужно, матрицы

строются следующим образом:

,
где

- октонионные структурные константы:

антисимметричны относительно перестановок любых двух индексов и равны нулю во всех остальных случаях.
Чую, что решение будет зависеть от трех произвольных функций.
Заранее спасибо за любые умные мысли.



