умножаем и дифференцируем p раз в F_p[x]/<x^p>

[maxal]

Старая задачка из sci.math.research

Пусть $p$ - простое и $F_p=\mathbb{Z}/p\mathbb{Z}$ - поле из $p$ элементов. Рассмотрим кольцо $R=F_p[x]/\langle x^p \rangle$, т.е. кольцо многочленов с коэффициентами из $F_p$ по модулю многочлена $x^p$.

В кольце $R$ определен формальный оператор дифференцирования, действующий на степенях $x$ очевидным образом:
$d x^n = n \cdot x^{n-1}.$

Пусть $f(x)$ - фиксированный элемент кольца $R$. Определим оператор $L:R\to R$ как
$L(g(x)) = d (f(x)\cdot g(x)).$

Две задачи:

1) Доказать, что $L^p = \alpha L,$ где $\alpha\in F_p.$

2) Определить значение $\alpha.$

[$]

Поясните, что вы обозначили за

\[ L^p \]

это p-я степень оператора L

\[ L^p (x) = L \circ L \circ \ldots \circ L(x) \]

?


Что то у меня подозрения, что ваше кольцо
является ни чем иным как полем Галуа из

\[ p^n \]

элементов.

Добавлено спустя 3 минуты 16 секунд:

Да да, ваше кольцо изоморфно полю Галуа. Открываю Ван дер Вардена "алгебру" на соответствующей странице про поля Галуа .

[maxal]

$ писал(а):

Поясните, что вы обозначили за

\[ L^p \]

это p-я степень оператора L

\[ L^p (x) = L \circ L \circ \ldots \circ L(x) \]

?

Да.

$ писал(а):

Что то у меня подозрения, что ваше кольцо
является ни чем иным как полем Галуа из

\[ p^n \]

элементов.

Нет. Многочлен $x^p,$ очевидно, является приводимым. Кольцо $R$ не является полем.

[$]

А на поле Галуа

\[ GL(p^n ) \]

можно смотреть как на линейное пространство над

\[ \mathbb{Z}/p\mathbb{Z} \]

- простым полем характеристики

\[ p \]

. С базисом

\[ \left\{ {1,x,x^2 ,...,x^{n - 1} } \right\} \]

, умножение- как умножение многочленов, с "правилом сокращения" (извиняюсь, забыл термин из теории групп что то вроде "определяющее соотношение")

\[ x^n = 1 \]

Добавлено спустя 3 минуты 45 секунд:

А разве не получается поле Галуа из

\[ p^p \]

элементов? То есть поле

\[ GL(p^p ) \]

?

[maxal]

$ писал(а):

с "правилом сокращения" (извиняюсь, забыл термин из теории групп что то вроде "определяющее соотношение")

\[ x^n = 1 \]

В данном случае правило другое: $x^p = 0.$

$ писал(а):

А разве не получается поле Галуа из

\[ p^p \]

элементов? То есть поле

\[ GL(p^p ) \]

?

Нет. Еще раз: R - это кольцо, не являющееся полем!

[$]

Совсем алгебру забыл. Ужас.

Добавлено спустя 4 минуты 48 секунд:

Цитата:

Нет. Еще раз: R - это кольцо, не являющееся полем!

Точно?

Вот я наверняка где то напутал.

Но чем ваше кольцо не поле Галуа? Вот этого то я понять не могу.

[maxal]

Сравните: $F_p[x]/\langle x^p - 1\rangle$ и $F_p[x]/\langle x^p\rangle.$
Первое является кольцом и в нем выполняется равенство $x^p = 1,$ второе является кольцом и в нем выполняется равенство $x^p = 0.$

[$]

(сам себе, размышления вслух), что конечное коммутативное кольцо без делителей нуля является полем.

Если вы мне напомните алгебру то буду думать над вашей задачей)))))

Добавлено спустя 58 секунд:

maxal писал(а):

Сравните: $F_p[x]/\langle x^p - 1\rangle$ и $F_p[x]/\langle x^p\rangle.$
Первое является полем и в нем выполняется равенство $x^p = 1,$ второе полем не является и в нем выполняется равенство $x^p = 0.$

Спасибо, теперь что то доходит о чем речь.

Добавлено спустя 15 минут 15 секунд:

Вот что я надумал, в каком направлении можно покопать. На досуге покопою.

Использовать формулу для n-ой производной произведения двух функций, к ней применить соотношения, выполняющиеся в вашем кольце, это может чего нибудь подсократит.

\[ (uv)^{(n)} = \sum\limits_{m = 0}^n {C_n^m u^{(m)} v^{(n - m)} } \]

Добавлено спустя 2 минуты 42 секунды:

В вашем случае это выглядит вот так (поменял буковку )

\[ (uv)^{(p)} = \sum\limits_{m = 0}^p {C_n^p u^{(m)} v^{(p - m)} } \]

Добавлено спустя 13 минут 44 секунды:

не туда пошло

Добавлено спустя 2 минуты 54 секунды:

Такой путь пробую. Написать явное выражение для

\[ L^p \]

в надежде, что там много сократится. Мы же имеем дело с многочленами над простым полем характеристики р.

Добавлено спустя 19 минут 10 секунд:

К слову L оказывается линейный. Поэтому достаточно доказать только равенство для базиса кольца многочленов (для соответствующих степеней х, которые в базисе). Так получается?

Добавлено спустя 7 минут 28 секунд:

А базис вашего кольца многочленов как линейного пространства из степеней х не выше р-1.

Добавлено спустя 7 минут 5 секунд:

Достаточно доказать, что

\[ L^p (x^s ) = \alpha L(x^s ),s \in \overline {0,p - 1} \]

так как то попроще выглядит, для случая если начинать расписывать L.

[Руст]

maxal писал(а):

Сравните: $F_p[x]/\langle x^p - 1\rangle$ и $F_p[x]/\langle x^p\rangle.$
Первое является полем и в нем выполняется равенство $x^p = 1,$ второе полем не является и в нем выполняется равенство $x^p = 0.$

Первое так же не поле. Полем является только Fp[x]/f(x)Fp[x] с неприводимым многочленом.

[maxal]

Да, заболтали. $F_p[x]/\langle x^p - 1\rangle$ - это кольцо, так как $x^p - 1$ делится на $x-1.$

[Дядя Фёдор]

maxal писал(а):

Старая задачка из sci.math.research

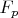
Пусть $p$ - простое и $F_p=\mathbb{Z}/p\mathbb{Z}$ - поле из $p$ элементов. Рассмотрим кольцо $R=F_p[x]/\langle x^p \rangle$, т.е. кольцо многочленов с коэффициентами из $F_p$ по модулю многочлена $x^p$.

В кольце $R$ определен формальный оператор дифференцирования, действующий на степенях $x$ очевидным образом:
$d x^n = n \cdot x^{n-1}.$

Пусть $f(x)$ - фиксированный элемент кольца $R$. Определим оператор $L:R\to R$ как
$L(g(x)) = d (f(x)\cdot g(x)).$

Две задачи:

1) Доказать, что $L^p = \alpha L,$ где $\alpha\in F_p.$

2) Определить значение $\alpha.$

Рассмотрим кольцо $R=F_p[x]/\langle x^p \rangle$ как векторное пространство и
оператор $L:R\to R$ как линейный оператор по второму полиному, пусть $M$ - его матрица, пусть теперь $F$ такое расширение поля в котором характеристический многочлен этой матрицы разлагается в произведение линейных многочленов и пусть тогда $MM$ его жорданова форма и $B$ матрица перехода к базису в котором матрица $L$ есть $MM$
тогда в нашем исходном базисе имеем матрица для $L$ это $B^{-1}*MM*B$ и для $L^p$ это $B^{-1}*MM^p*B$
самая большая жорданова клетка может быть размером с матрицу и её степень будет иметь
вид $J_{i,j}= (\alpha_k^{p-j+i}*C_p^{j-i})*\delta(j>=i)$
но так как поле имеет характеристику p, то все внедиагональные элементы будут нулями а на диагонали \alpha_k^p которые опять же в силу характеристики поля равны \alpha_k под \alpha_k^p мы подразумеваем собственное значение номер к, которое мы не станем здесь вычислять. Тем не менее при любом числе \alpha разность $L^p-L$ с матрицей $B^{-1}*(MM^p-\alpha*MM)*B$ есть ноль только если ММ тоже диагональная и \alpha = 1 или \alpha = 0 другими словами других \alpha кроме 0 и 1 быть не может, действительно при $f(x)=\beta*x$ собственное значение 1 и при $f(x)=\beta*x^n$ при n не равном 1 это 0
Осталось аккуратно проверить что будет происходить когда есть например степень ноль и степень 2, то есть степени симметричные по отношению к 1, в силу того, что тогда коэффициент будет зависеть от коэффициентов при этих степенях, надо завтра посчитать что будет происходить - один будет понижать а второй повышать степень, здесь тоже должна получиться единица или ноль

[Руст]

Зачем так усложнять. Если взять базис $\frac{x^k}{k!}$, где k! считается как обычный факториал за исключением множителей делящихся на р, например (2р)!=(2p-1)...(p+1)(p-1)...1. В этом базисе оператор дифференцирования имеет форму Жордановой клетки с нулевым собственным значением, т.е. оператор полученный вначале умножением, а потом дифференцированием, так же будет иметь нулевое собственное значение. Соответственно $\alpha $ может быть только нулём.

[RIP]

Если $p=2$ и $f(x)=x$, то $\alpha=1$.

[Руст]

RIP писал(а):

Если $p=2$ и $f(x)=x$, то $\alpha=1$.

Да при любом p в случае $f(x)=x^k$ число $\alpha =\delta_k^1$, хотя и имеются собственные значения равные нулю. Вообще, если f(x) не имеет свободного коэффициента, т.е. $f(x)=a_1x+a_2x^2+...+a_kx^k$, то матрица L имеет нули выше диагонали и легко просчитывается $L^p=\alpha L, \ \alpha=1-\delta_{a_1}^0.$

[Дядя Фёдор]

Дядя Фёдор писал(а):

Осталось аккуратно проверить что будет происходить когда есть например степень ноль и степень 2, то есть степени симметричные по отношению к 1, в силу того, что тогда коэффициент будет зависеть от коэффициентов при этих степенях, надо завтра посчитать что будет происходить - один будет понижать а второй повышать степень, здесь тоже должна получиться единица или ноль

вношу поправку - дело в том, что расширение степени к будет иметь мултипликативную группу из p^k - 1 элементов и там конечно будут элементы цтепень которых не есть р, так что будут и другие собственные значения.