Хм... Не поленился, написал решение

Для каждого натурального

пусть

такая функция, что

для всех

и

. Пусть теперь

--- натуральные числа и даны вектора

,

. Надо найти их скалярное произведение

1) Числа

и

--- нечётные взаимно простые. Пусть для натурального

отображение

есть канонический гомоморфизм абелевой группы

в абелеву группу

. Так как

и

взаимно просты, то

--- порождающая циклической абелевой группы

. Пусть для
![$i \in [1,pq]$ $i \in [1,pq]$](https://dxdy-02.korotkov.co.uk/f/9/9/e/99efdf560a9c7bbbe435c9f2a3f5963982.png)
число

равно целому числу из отрезка
![$[1,p]$ $[1,p]$](https://dxdy-02.korotkov.co.uk/f/9/0/b/90b67c3c9e2ed66cb580092c01be0afa82.png)
, такому что

(фактически

равно остатку от деления

на

, к которому, если он равен

, прибавлено

). Аналогично пусть

--- целое число, такое что

и

. Нетрудно видеть, что каждое
![$i \in [1,pq]$ $i \in [1,pq]$](https://dxdy-02.korotkov.co.uk/f/9/9/e/99efdf560a9c7bbbe435c9f2a3f5963982.png)
расписывается в виде

. Но тогда

и, в силу нечётности

и

, выполняется

. Но тогда

2) Числа

и

разной чётности. Заметим, что

и, аналогично,

для всех

. Для
![$i \in [1,pq/2]$ $i \in [1,pq/2]$](https://dxdy-03.korotkov.co.uk/f/e/6/b/e6b2e8de14b9526021621b92387c653582.png)
получаем

и

3) Пусть

--- произвольные ненулевые натуральные число. Сначала заметим, что для любых натуральных

,
![$i \in [1,s]$ $i \in [1,s]$](https://dxdy-02.korotkov.co.uk/f/5/6/e/56e5001c866e622c0616d807ee057f2c82.png)
и целого

выполняется

. Действительно, при данных условиях и
![$j \in [1,r]$ $j \in [1,r]$](https://dxdy-04.korotkov.co.uk/f/f/c/1/fc1cd406de6c4df65b8fb12ac6c091dd82.png)
выполнено

, а добавляя к

число

, мы увеличиваем аргумент

на
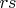
. Отсюда получаем

Далее, для любого

справедливо

, так что

Теперь если число

чётное, то сумма по

равна

и

. Если же

нечётно, то

и

разной чётности,

,

и всё равно

. Во всех случаях получаем




