И не просветите, что такое радиальная ограниченность?
По контексту радиальная
неограниченность -- это стремление к бесконечности при

. На биссектрисе

это нарушается.
Кстати, контрпример, на мой взгляд, чересчур изыскан в своей конкретности. Достаточно взять любую ограниченную функцию

, положительную при

и равную нулю в нуле. И любую функцию

, положительную на
![$[0;{2\pi}]$ $[0;{2\pi}]$](https://dxdy-03.korotkov.co.uk/f/2/0/d/20d8058061856690f7dee09fadb01ca182.png)
всюду, за исключением одной или нескольких точек (в которых она равна нулю), не совпадающих с

. И рассмотреть функцию
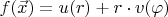
(в полярных координатах).