Извиняйте, что по техническим причинам на аглицком языке.
DELTA VECTOR IN ALGEBRAS WITH CONVOLUTION
Delta function is a very often used term. It is a convenient math object for efficient solution of wide spectrum of scientific tasks. But some problems are possible when we use delta function. For example usage of such math object can be a reason of mutually exclusive solutions for the same task and so on.
The main idea of this paper is to find other function that has the delta function's properties. Because this new function is not the delta function so it has to be some limitations for using a new method. For example this new function can has delta function's properties for some limited set of other functions only.
Let
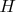
is the Hilbert space and

,
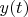
,
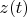
are vectors of this space:

We consider vectors in
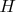
are real functions of the real argument.
Because
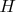
is the Hilbert space so there is an inner product for any two vectors of this space too.
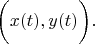
Let we build the convolution with the inner product.
Definition 1. A convolution of two Hilbert space's vectors is a third vector of this space which is calculated by following formula:
It is possible to prove the commutativity property of this convolution.
Lemma 1. The convolution of two Hilbert space's vectors has the commutativity property: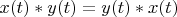
.
Proving.
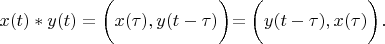
Using this substitution:
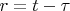
and
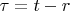
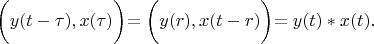
Lemma 1 is proved.
Of course the delta function cannot be a vector of Hilbert space because norm of delta function is infinity. So our target is finding such function that has following very important delta function property:
 Definition 2. Delta vector of Hilbert space with the convolution is such vector
Definition 2. Delta vector of Hilbert space with the convolution is such vector 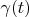 that has following property:
that has following property: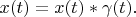

is any vector from
.
Delta vector is defined. Now it is necessary to calculate one.
Theorem 1. If Hilbert Space with orthonormal basis 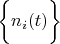 consists a delta vector
consists a delta vector 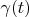 then this vector can be calculated by formula:
then this vector can be calculated by formula: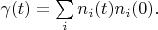
Proving. Let

is a vector in
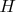
and
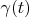
is the delta vector of
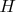
, so in accordance with definition 2:
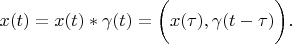
Expanding vectors
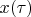
and
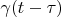
in basis
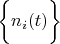
:


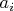
and
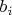
are expansion coefficients. In accordance with Parseval's identity it is possible to write:
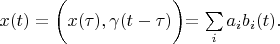
Expanding vectors

in basis:
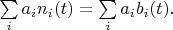
So we can write:
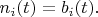
Therefore:

and

The theorem is proved.
For the reason of theorem 1 it is possible to deduce two conclusions.
First. The delta vector always exists in finite Hilbert space. Infinite Hilbert space contains this vector if
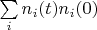
is convergent series only. For example, Hilbert space of functions that are defined on finite segment
![$ \biggl [ - \frac {1} {2} , \frac {1} {2} \biggl ] $ $ \biggl [ - \frac {1} {2} , \frac {1} {2} \biggl ] $](https://dxdy-04.korotkov.co.uk/f/7/a/1/7a19010c42bfe1783ea6a846d38f808a82.png)
expands in the basis
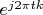
. It is obvious that the series
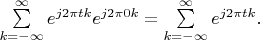
is divergent one at point

. So the delta vector is absent in this Hilbert space.
Secondly. Really, the delta vector can be absent in some Hilbert spaces but the interpolating operator

always exists if function

is defined in the point
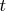
. Dirac said that delta function can exist under integral sign only. Using a paraphrase we could say that the delta vector can exist under inner product sign.
Proving of some delta vector properties is present below.
Lemma 2. Square of norm (energy) of delta vector equals 
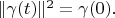
Proving.

Using this substitution:
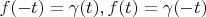
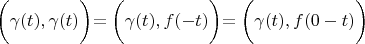
Using lemma 1:
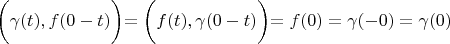
Lemma is proved.
This property of delta vector corresponds to intuitive understanding that norm of delta function is infinity:
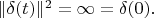
Discuss the symmetry property of delta vectors.
Lemma 3. For any delta vector, the following expression is truly 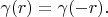
Firstly we will prove that
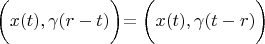
for any

.
For formula
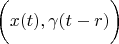
we use such substitution
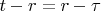
and

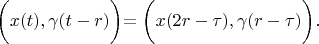
According definition 2:
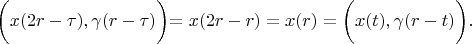
Therefore
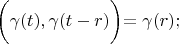
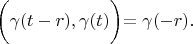
According definition 1:

So

Lemma is proved.
If some Hilbert space has a delta vector
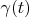
then there is a full orthogonal basis
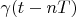
. Below we will discuss this thesis.
Let there is a bijection of functional Hilbert space
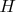
with convolution on other functional Hilbert space
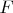
. We add a proviso: every vector

corresponds to alone vector
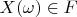
and convolution of any two vectors

,

corresponds to product of two vectors
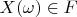
,
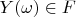
.

Apparently delta vector
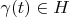
has to correspond to vector
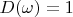
on definitional domain of space
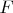
(this domain can beset of segments). It is necessary to obey condition
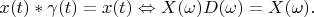
It is easy to show that
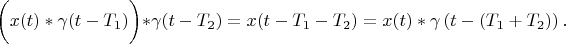
Therefore:

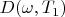
corresponds to
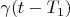
;
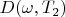
corresponds to
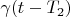
;
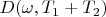
corresponds to
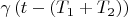
. So we can write:
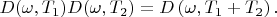
Finding logarithm:
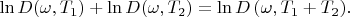
Differentiating with respect to
:
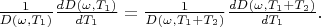
From derived expression we see that:
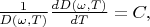
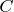
-- constant is depended from
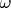
.
Therefore:
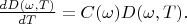
Apparently that this equation solution is the function
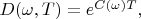
Let discuss the function

. On the assumption of Parseval's identity and lemma 2 we can write following expression:
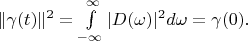
From this expression and condition
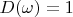
it is possible to find Lebesgue measure for

. This Lebesgue measure is

. Now it is possible to prove a theorem.
Theorem 2. If functional Hilbert space has a delta vector 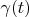 then this space has full orthogonal basis
then this space has full orthogonal basis 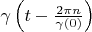 too.
too.Proving. There is a bijection of functional Hilbert space
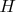
with convolution on other functional Hilbert space
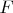
. This bijection is Fourier transform. In this case convolution of two vectors in
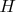
corresponds to product of their spectrums in
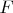
. If space
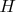
contains delta vector
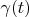
then according to reasoning that is placed before all vectors in
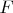
have finite support. Against norm of
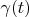
is infinite. Therefore all vectors in
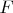
can be not equal zero on the segment with total length

.
Transform space
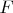
in the following way: all segments of the axis
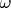
where vectors can be not equal zero are been shifted close each other. Total segment (one's length is
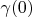
) is placed from point
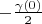
to point
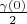
. Thereby all vectors from new space are expanded in the basis Fourier

on the segment
![$ \left [ - \frac {\gamma (0)} {2} , \frac {\gamma (0)} {2} \right ] $ $ \left [ - \frac {\gamma (0)} {2} , \frac {\gamma (0)} {2} \right ] $](https://dxdy-04.korotkov.co.uk/f/b/5/a/b5a26b0bd862129fe4290cdffdf31fdc82.png)
. The basis Fourier

is full basis. As it has been shown before the delta vector
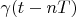
corresponds to
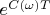
therefore
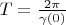
and
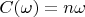
. Because
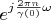
is a full basis so correspondent vectors
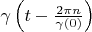
are full basis too.
Theorem is proved.
Now let we will discuss interpolated possibility of the delta vector.
Theorem 3. If functional Hilbert space has a delta vector 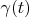 then any vector
then any vector  in this space can be interpolated with its samples
in this space can be interpolated with its samples  by the following formula:
by the following formula: 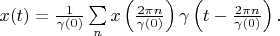
Proving. According to theorem 2
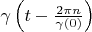
vectors are the orthogonal basis in
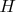
. Therefore any vector
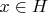
can be presented as
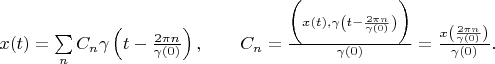
Therefore
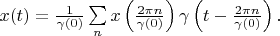
The theorem is proved.
Introduce an area definition for vectors in
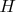
.
Definition 3. ![$Area of a vector [math]$ x $ $Area of a vector [math]$ x $](https://dxdy-04.korotkov.co.uk/f/7/b/2/7b297477a304d5ec5181efc86d3c25c082.png)
is the functional$[/math]
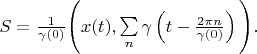
Now we can prove next delta vector's property.
Lemma 4. Delta vector's area is always 1. Proving. According definition 3
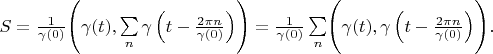
Because vectors
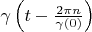
and
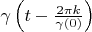
are orthogonal if
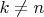
so their inner product is zero. Therefore
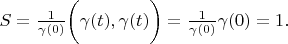
The lemma is proved.
Let we present an example of Hilbert space with a delta vector. This space is the set of all functions with finite spectrums that are not zero on segment
![$ [ -\Omega , \Omega ] $ $ [ -\Omega , \Omega ] $](https://dxdy-02.korotkov.co.uk/f/5/2/c/52c823f356395c442ab690a5b00f003082.png)
only. Of course norms of these functions are limited too. Inner product for any two vectors of this space is the following expression:

According definition 1 and definition 2 it is correct to write:
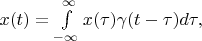

is any vector of this space.
This expression is a classical convolution of two functions

and
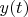
Note: classical Dirac delta function is not a delta vector because one's spectrum is not limited by the segment
![$ [- \Omega , \Omega] $ $ [- \Omega , \Omega] $](https://dxdy-01.korotkov.co.uk/f/c/f/9/cf9add6ebfd6d62910dd18a23e1d887882.png)
so this function is not a vector of the presented space. It is necessary to find delta vector among functions with a finite spectrum.
It is well known that convolution of two functions corresponds to product of their spectrum. Let we find such function
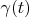
with spectrum

that has following property:
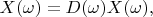
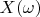
is spectrum of any vector in the presented space.
Apparently that
![$ D(\omega)= \left \{ \begin {array} {l}
1, \; \omega \in [-\Omega , \Omega ] \\
0, \; \omega \notin [-\Omega , \Omega ]
\end {array} \right.$ $ D(\omega)= \left \{ \begin {array} {l}
1, \; \omega \in [-\Omega , \Omega ] \\
0, \; \omega \notin [-\Omega , \Omega ]
\end {array} \right.$](https://dxdy-03.korotkov.co.uk/f/2/4/7/24756722ce44449d2bc142ce960b4fa682.png)
Only one function has such spectrum:
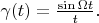
It is well known that functions
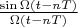
are an orthogonal basis for presented space. For this case:
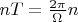
,
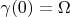
,

. And interpolated theorem 3 for our space has following form:
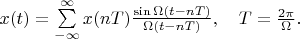
This is famous Shannon's theorem.