Добрый день, помогите пожалуйста придумать пример. Есть процесс Ито (диффузия) вида

И функция

. Нужно придумать пример, чтобы задача оптимальной остановки
![$$
V(x) = \sup\limits_\tau \mathbb{E}_x[h(X_\tau)]
$$ $$
V(x) = \sup\limits_\tau \mathbb{E}_x[h(X_\tau)]
$$](https://dxdy-04.korotkov.co.uk/f/f/3/a/f3aa85f4c392ccbd9f3cfb6be193620082.png)
решалась аналитически. Т.к. процесс однородный марковский, то можно это переформулировать в задачу с подвижной границей в

. Считаем генератор процесса

, полчаем

То есть нужно решить следующую задачу:

на

,

на

.
Я беру устойчивый процесс

, где

. По симуляциям очень хорошо видно, что процесс сходится к нулю довольно быстро (при

обычно очень близко к нулю при

).
Так как мы хотим получить значение

чем больше, тем лучше - значит пока значение квадрата большое, надо остановится, так что я ищу множество

в виде
![$x\in(-\infty,a]\cup[b,+\infty)$ $x\in(-\infty,a]\cup[b,+\infty)$](https://dxdy-03.korotkov.co.uk/f/2/5/0/25083543372768016b3695c637ff5ee082.png)
. В итоге у меня получается, что я сначала решаю

на неизвестном промежутке
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
, получаю общее решение с двумя неизвестными

(решение этой задачи легко получить аналитически, хоть там и противные функции).
Потом я накладываю условия гладкости и непрерывности в точках

и

- итого 4 условия на 4 неизвестных, и должно получиться нормальное решение. Здесь я уже могу решать только численно - и в ответ всегда получаю, что
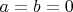
. И это для очень многих типов процессов, которые я рассматривал, не только

.
Вопрос собственно такой:
1. у меня получается, что квадрат любого процесса Ито нужно сразу останавливать (что скорее всего ошибка)
2. в чем тогда заключается ошибка
3. какой пример придумать, чтобы задача хорошо решалась (единственное условие -

и что процесс

-диффузия = процесс Ито).



