Это я знаю, но смотрится не очень.
"Очень" или "не очень" -- это довольно субъективно. Кто к чему привык, то тому и "очень".
что обозначают
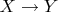
и

(в

и

соответственно)? Лично я бы назвал первое -- множеством (классом) функций из

в

, а второе -- некоторой фиксированной функцией, но судя по тому, что используется

вместо

и

соответсвенно, что-то другое под теми обозначениями понимается
Да ничего особенного под теми обозначениями не понимается; просто в первом случае описание функции строится как
<название> ':' <множество> '

' <множество>
а во втором запись

означает

. На мой взгляд, не надо искать здесь какой-то дополнительный смысл.
Т. е. добавление индекса "0" фиксирует аргумент?
Математические формулы пишутся для людей, а люди в состоянии понять смысл из контекста или из явного указания. В данном случае -- да: в записи

индекс

означает, что мы фиксируем значение второй переменной равным

и таким образом получаем функцию одной переменной.
Вот как бы вы записали формулу Тейлора через дифференциалы...?
Не очень понял, что я должен записать, а главное -- зачем. В каких, на Ваш взгляд, конкретных случаях частично-применённые функции позволят получить более удобную запись?



