Инъекции и сюръекции в Set

[caxap]

Верно ли я понимаю, что в категории множеств ($\mathrm{\bf{Set}}$) инъекция = сечение (section) = мономорфизм, а сюръекция = ретракция = эпиморфизм?

(P. S.)

Инъекция -- отображение, не склеивающее точки ($a\neq b\Rightarrow f(a)\neq f(b)$). Cюръекция -- отображение "на".
Сечение -- имеет левую обратную функцию, ретракция -- правую обратную.
На мономорфизм можно сокращать слева ($m\circ f = m\circ g\Rightarrow f=g$), на эпиморфизм -- справа.

[id]

Да.
Оно и в $\mathrm {Lin}$ верно, кстати.

[caxap]

id
Ясно. Спасибо. (А что такое $\mathrm{\bf{Lin}}$? Линейные пространства?)

Помогите, пожалуйста, доказать всё это. Мои попытки:

(инъекция = мономорфизм)

$\Rightarrow$
Рассмотрим мономорфизм $m\colon X\to Y$ и два произвольных элемента $a,b\in X$. $a$ и $b$ можно отождествить с константными функциями. Тогда $m(a)=m(b)\Leftrightarrow m\circ a = m\circ b \Rightarrow a=b$ (сокращаем слева). А значит $a\neq b\Rightarrow m(a)\neq m(b)$, т. е. $m$ -- инъекция.

$\Leftarrow$
Пусть $m$ -- инъекция, тогда $m(a)=m(b)\Rightarrow a=b$, что равносильно сокращению на $m$, значит $m$ -- мономорфизм.

(инъекция = сечение)

$\Rightarrow$
Пусть $m\colon X\to Y$ -- инъекция, т. е. переводит разные элементы в разные. Каждому такому отображению элемента $X\ni x\mapsto y\in Y$ сопоставим отображение $Y\ni y\mapsto x\in X$. Совокупность таких отображений $r\colon Y\to X$ и будет левой обратной функцией, т. к. $r\circ m = \mathrm{id}_X$.

$\Leftarrow$
$m$ -- сечение, т. е. имеет левую обратную функцию $r$. Но чтобы $r$ была обратной для $m$, $m$ не должна "склеивать" точки, т. е. должна быть инъекцией. (Тут строго я не знаю как показать, но интуитивно вроде понимаю )

(сюръекция = эпиморфизм)

Вот тут я не соображу

(сюръекция = ретракция)

$\Rightarrow$
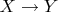
Пусть $e\colon X\to Y$ -- сюръекция, значит несколько элементов из $x$ могут переходить в один элемент из $Y$. Для каждого элемента из $Y$ выберем (неважно как) только одно отображение некоторого элемента из $X$ в него (т. е. уберём все "склеивания"). Получим функцию $X\to Y$, которая будет уже биекцией, поэтому будет существовать правая обратная функция $s$ такая, что $e\circ s=\mathrm{id}_Y$.
$\Leftarrow$Пусть $s\colon Y\to X$ -- правая обратная функция для $e$. Она определена на всем $Y$, т. е. функция $e$ будет отображением "на", или сюръекцией.

P. S. Такая путаница с этими -екциями и -измами. Нет ли какого-нибудь мнемонического правила, чтобы всё это запомнить? (Да ещё слова какие-то не самоописательные, ну инъекция-то ещё ладно, а вот сюръекция (что за "сюр"?), мономорфизм (почему "моно", что там 1?), эпиморфизм (эпи?)...)

[Padawan]

caxap в сообщении #369501 писал(а):

$\mathrm{\bf{Lin}}$? Линейные пространства?

Точнее линейные пространства и линейные отображения между ними.
Аналогично $\mathbf {Set}$ -- множества и отображения между ними.

[Joker_vD]

"sur" — лат. и фр. "на"; "эпи" — др.-греч. "на, над". Сюръекция, эпиморфизм — отображение на.

[caxap]

(Оффтоп)

Joker_vD в сообщении #369545 писал(а):

"sur" — лат. и фр. "на"; "эпи" — др.-греч. "на, над". Сюръекция, эпиморфизм — отображение на.

Ух ты. Спасибо. Сразу вспомнил "эпиграмма", "эпитафия". Теперь не забуду!
Мономорфизм, как я понял -- потому что инъекция отображает "один элемент в один". (В вики прочитал, что моно-, эпи- и биморфизм в теории категорий являются обобщением соотв. инъ-, сюръ и биекции в теории множеств. Так бы сразу )

Осталось выяснить, почему ретракция (en. retraction) и сечение (en. section) так называются.