Как я понял, Вам необходимо принять решение, будет ли увеличена прибыль (данная целевой функцией) если добавить новый вид продукции (дополнительная переменная). Пусть дана задачи линейного программирования




-

вектор,

-

вектор,

-
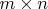
матрица,

-

вектор. После решения задачи получаем оптимальное решение

, где

- оптимальный базис. Если

, то решение оптимальное.
Теперь добавляете ещё одну переменную. Задача становится следующей



Если

, то полученный до этого базис является оптимальным и оптимальное решение не выпускать продукцию. Если же

, то прибыль может быть увеличена, если выпускать новый вид продукции. Поэтому добавляете дополнительную колонку в симплекс-таблицу и ищете новое оптимальное решение.



