(Оффтоп)
А что если мера не
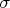
-конечна? Будет ли полно пространство

?
А что такое в таком случае

?
А что не так с

? Понятие интеграла Лебега определено (скажем, для неотрицательной функции это супремум интегралов от простых функций, не превосходящих данную), буквосочетание

тоже ...
З.Ы. Кажется, я понял. Если измеримая функция на таком пространстве будет в

, то найдется такое множество

, что
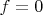
вне

, а мера
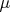
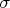
-конечна на

. Тогда для всякой фундаментальной последовательности

возьмем

, и на их объединении тоже получится
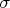
-конечная мера. (Я еще не всё тут подумал - так, бросок мысли)
(Фтоп)
А для интеграла Римана даже критерий есть
 post124766.html#p124766
post124766.html#p124766З.Ы. Писалось в те старые добрые времена, когда двойные доллары еще не выставляли формулу на отдельную строчку.



