Решаю задачку из вышеупомянутой книги, не сходится.
Рассмотрим интервал
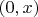
на котором равномерно распределены точки

. Случайно выберем одну из них такую, что

и построим интервал

. Обозначим выбранную левую точку через

.
Далее, если уже построены интервалы

, случайно выберем следующую точку

из

. Если удается построить интервал с левой точкой

(лежащий внутри
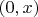
и не пересекающий предыдущие интервалы), то обозначим его

(а выбранную левую точку

- через

). Если нет - выбираем следующую точку из

.
Обозначим через
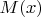
ожидание

, где

- число интервалов, которое удалось запаковать в
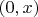
процедурой выше.
Требуется показать, что

;

У меня получилось несколько другое уравнение, а именно:
Рассмотрим

. Тогда

. Положим

; тогда

.
Мне кажется, что

(но я это строго не доказывал). Тогда

Что неверно?



