ewert писал(а):
нет, честно говоря, не хочу. Да и вот: тов. Лукомор -- а он известный провокатор -- и тот только что за правильное решение проголосовал.
Кто провокатор - я?

Давайте еще раз, по пунктам:
.
1). Игрок выбирает дверь, за которой автомобиль, с вероятностью

,
либо дверь за которой нет автомобиля с вероятностью

.
.
2). Ведущий выбирает дверь за которой автомобиль с вероятностью 0,
либо дверь за которой нет автомобиля с вероятностью 1.
.
3). За никем не выбранной дверью автомобиль находится с вероятностью

.
нет автомобиля с вероятностью

.
.
Проверяем:
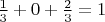

--------------------------------------------------------------
 Добавлено спустя 5 минут 21 секунду:
Добавлено спустя 5 минут 21 секунду:Если выбор ведущего случаен (не знает где пустая дверь), то вероятность события "дверь оказалась пустой" равна 2/3.
Ведущий знает, где находится автомобиль.
Ведущий никогда не открывает дверь, за которой находится автомобиль.



