Это всё потому, что возведение обеих частей равенства

в куб:

и подстановка

, что здесь делалось, приводит к

.
Поскольку

, то это фактически
домножение обеих частей равенства

на

.
Такое преобразование будет эквивалентным, когда

или когда корень

является корнем исходного уравнения.
Последнее неравенство означает, что среди чисел

,

и

имеются различные.
То бишь если мы не хотим делать в конце тотальную проверку, то вначале надо проверить,
является ли корень системы
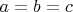
корнем исходного уравнения.
Если да является (такое бывает!), то преобразования будут эквивалентными.
Если нет, - то мы его забракуем в конце.
Если же у системы
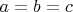
нет корней, то тогда тем более преобразования будут эквивалентными.