Здравствуйте.
Задача по ТФКП. Вычислить несобственный интеграл с помощью вычетов.
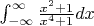
Собственно решение ищется по известной формуле
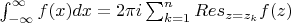
Осталось найти вычеты ))
Я разложил знаменатель на множители, подинтегральная функция стала выглядеть так:
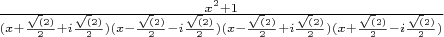
Выходит есть 4 особые точки, из которых нам нужны только 2 (я правильно понял, что берём только те что лежат в верхней полуплоскости??). Обе точки полюсы, первого порядка.
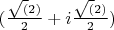
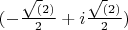
Считаем первый вычет, получаем, вот такую штуку.
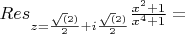
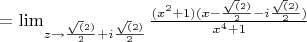
Не знаю с какой стороны подойти к этому пределу. И верен ли в целом ход решения?



