Интеграл Мора для составной балки с промежуточными шарнирами

[eugrita]

Вопрос касается метода вычисления прогиба с помощью перемножения эпюр (интеграла Мора) в случае балки с промежуточными шарнирами.
1)можно ли вообще применять этот метод рассматривая составную балку как цельную
2)если да,то как надо перемножать грузовую и единичные эпюры : - по всей ли длине составной балки или только по каждой балки входящей в состав?
3)Как строить единичную эпюру каждого участка? При определении прогиба в шарнире надо приложить к нему $P=1$ при этом поперечная сила участков и единичная эпюра зависит не только от $P $ но и от реакции шарнира $R $.
Рассмотрим пример Пусть балка защемлена с 2 концов и имеет 1 шарнир
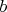
(длина левой части $a$, правой $b $ (общая длина $l=a+b$ )
Несложный расчет даст выражение силы реакции шарнира $R_1_2$
(cчитаем $a<b$ и реакцию $R$ для левого участка направим вниз как и $P$)
из условия равенства прогибов 2 простых балок $R_1_2=P\frac{1-k^3} {1+k^3}$ $k=\frac a b$
и выражение прогиба в шарнире: $v=\frac {2P} {3EI} \frac{k^3a^3}{1+k^3}$
Проверка показывает что такой же результат получим при применении перемножения эпюр $M_1$ и $M_p$
а)только левой балки $0\leq x \leq b$(Если учесть и участок$ b$, получим другой результат!).
б)в качестве единичной эпюры 1 участка берем интеграл от эпюры поперечных сил$P=1$ (ни в коем случае не $P-R_1_2$)
Детали см. на рисунках:



Выводы
предположения а) и б) при вычислении прогиба мне лично самому показались неожиданными: (ни в одном известном мне курсе сопромата не описаны), но при всем при этом дали верный результат. Классический метод построения единичной эпюры разбираемый в курсах сопромата состоит в приложении единичной силы P=1 и далее после определения всех реакций от нее построения единичной эпюры изгибающих моментов - а здесь:
1) только для части конструкции 2)запрет учета реакции в шарнире
Так ли все это и правильно ли я понимаю особенности применения перемножения эпюр для этого и аналогичных случаев балок соединенных шарнирами?

[Парджеттер]

Тема перемещена из Механики и Техники
Физики в Карантин по следующим причинам:
- формулы надо набирать в нотации $\TeX$. Как это делать можно посмотреть в теме Краткий ФАК по тегу [math].
- вы когда-нибудь в книгах видели звёздочки в качестве знака умножения? В набранных формулах уберите звездочки;
- не допускается выкладывать картинки, которые можно заменить текстом или формулами;
- картинка, если ее необходимо использовать, должна быть видна без похода на сторонние ресурсы;
- вообще этот монолог мне не нравится. Оформите всё как единый и связный текст. Если вам не отвечают, значит либо не могут, либо не хотят, либо, что чаще всего бывают, Вы плохо изложили суть вопроса.

Исправьте все Ваши ошибки и сообщите об этом либо при помощи личного сообщения модератору, либо в теме Сообщение в карантине исправлено.

Рекомендую также прочитать тему Что такое карантин и что нужно делать, чтобы там оказаться - там описано за что можно попасть в Карантин и как исправлять положение.

Также в качестве полезного чтения рекомендую Правила научного форума.

[Парджеттер]

Возвращаю.