ДОброго времени суток!
Вошел в ступор при решении следующего примера:
Найти наименьшее и наибольше значение функции

в замкнутой области Д, заданной системой неравенств

Сперва нашел стационарные точки. Получилась точка (0;0), в которой функция экстремума не имеет. Далее записал уравнение связи исходя из неравенств, Так как неравенства ограничивают прямоугольник площадью 6, то у меня получилось следующее уравнение

Далее составил функцию

и исследовал ее на экстремум. получил снова точку (0;0) при
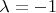
. В итоге у меня получилось, что экстремумов нету.
А как найти тогда наименьшее и наибольшие значения? Я не понимаю, как мне пробегать область, заданную неравенствами и и смотреть значения функции z в данных точках. ПОдскажите пожалуйста!



