Имеется связный граф из

эквивалентных друг другу вершин и

эквивалентных друг другу рёбер, в котором каждая из вершин соединена четырьмя рёбрами с четырьмя другими вершинами.
Этот граф очень удобно рассматривать, натянув его на единичную

-сферу так, что длины всех рёбер равны. Декартовы координаты

вершин в

-пространстве при этом можно задать следующим образом (

):

Все чётные перестановки

(всего

вершин)
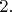

(всего

вершин)
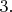
Все перестановки

(всего

вершин)

Все перестановки

с чётным количеством знаков "минус" (всего

вершины)

Все перестановки

с нечётным количеством знаков "минус" (всего

вершины)

Все перестановки

с чётным количеством знаков "минус" (всего

вершины)

Все перестановки

(всего

вершины)
Раскрасим

вершин из первых трёх пунктов в белый цвет, а остальные - в чёрный. Оказывается, белые вершины являются вершинами правильного
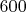
-ячейника (см.
вики), причём в каждой пятой тетраэдрической ячейке сидит чёрная вершина. Аналогичным образом чёрные вершины являются вершинами другого правильного
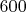
-ячейника, в

ячеек которого сидят белые вершины. Каждое ребро графа соединяет вершины разного цвета; длина ребра составляет

, а расстояние между ближайшими одноцветными вершинами равно

и является длиной ребра
-ячейника.
Вся

-вершинная конструкция является хиральной, т.е. если мы сменим чётность количества знаков "минус" в пунктах

,

и

списка координат, то полученное зеркальное отражение нельзя будет совместить с первоначальным графом с помощью одних лишь

-поворотов.
Вот так (или зеркально) выглядят ближайшие

соседей белой вершины (помечена единичкой):
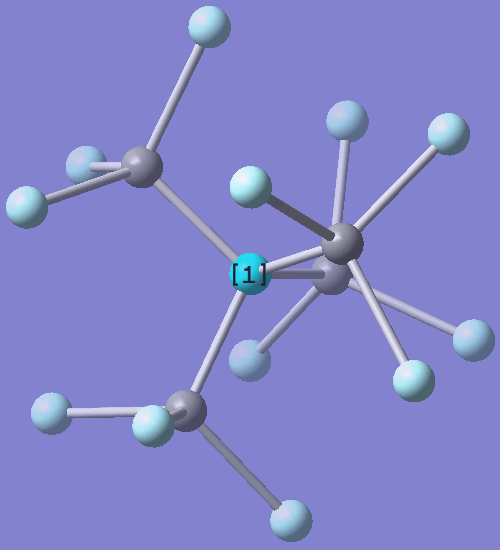
Видно, как для белой вершины ближайшие чёрные образуют правильный тетраэдр, а ближайшие белые - икосаэдр.
А вот так (или зеркально, опять же) выглядят ближайшие

соседей:
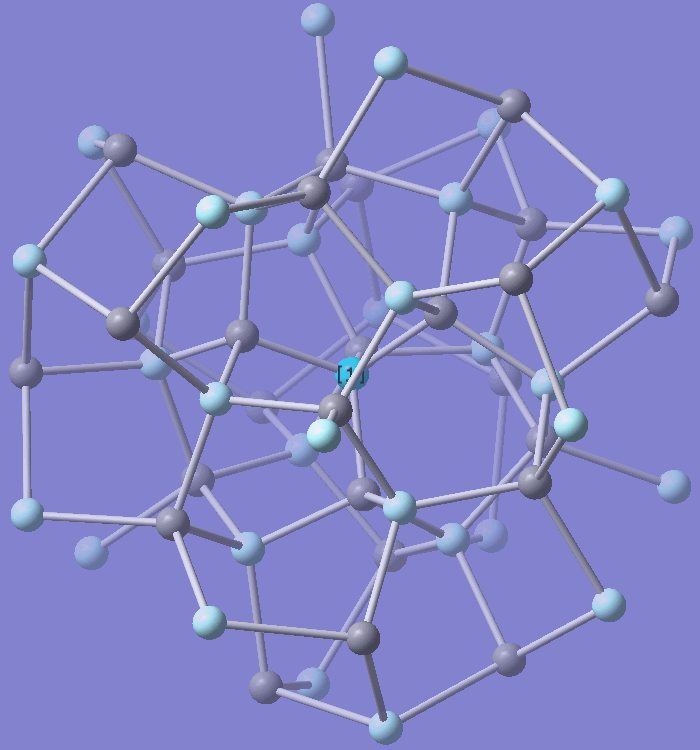
Отчётливо видны шестичленные циклы (всего их

); в каждом таком цикле одна пара вершин находится на расстоянии

, а остальные пары теснее.
На этом "поле" можно создать аналог игры "го".
* * * * * * *
Мне так кажется, что такой симметричный граф уже должен быть известен и изучен. Есть ли какая-то информация о нём?