Поворот на клетчатом листе

[Circiter]

2VoloCh

Цитата:

А вот вам похожая по духу задача.

Я периодически занимаюсь этой задачей. Она до сих пор не решена (по крайней мере в исходной постановке).

Кстати, у меня есть кое-какие наброски одного метода, который мог бы помочь в анализе/решении этой задачи, но отполировать мысли и поделиться предварительными результатами я смогу только через пару месяцев... Пока же могу сказать, что в основе моего метода лежит известный прием с обращением условия этой задачи (путем сведения её к задаче о возможности сконструировать любое натуральное число из единицы последовательностью операций, обратных к исходным) с последующим её анализом в одной хитрой системе счисления при помощи одной не менее хитрой машины... :)

Ещё я к ней придумал одну на мой взгляд забавную тополого-геометрическую аналогию, но боюсь, что она может быть ошибочной... Во всяком случае, о ней мне рассказывать тоже пока рано... :)

[Circiter]

Вопрос (нешибко существенный) по основной теме. Можно ли утверждать, что угловой "пробег" точки (сумма приращений угла точки в полярных координатах на каждой итерации с учетом знака) либо неизменяется, либо строго возрастает, либо строго возрастая с начала моделирования после определенного момента неизменяется? Вроде бы очевидно, или нет?...

[VoloCh]

Я, извините, не понял вопроса. Угол поворота (по основной задаче) - строгая константа. Конечно, округление этот угол чуток подправит. И чем больше начальный радиус, тем эта поправка меньше.

Я хочу сказать вот что: пусть $x_n$ - исходная последовательность и $(r_n,т\beta_n)$ - ее полярные координаты. Надо доказать, что $r_n$ - ограниченная последовательность. Если есть контрпример, то для этого примера, очевидно, $\beta_n\to\alpha$. А в наблюдаемых "орбитальных случаях" (когда радиус-вектор болтается в полосе $[R_1,R_2]$) будет выполнться $|\beta_n-\alpha|<\varepsilon_R$. Чем больше радиус орбиты $R$, тем меньше $\varepsilon_R$ (при очень маленьких радиусах $\varepsilon_R=\frac{\pi}2$ (либо $x_n$ свалится в 0).

[paha]

я перестал за топиком следить...

VoloCh в сообщении #306783 писал(а):

Если есть контрпример, то для этого примера, очевидно, $\beta_n\to\alpha$

а вот почему?

VoloCh в сообщении #306783 писал(а):

(либо $x_n$ свалится в 0)

разве кто-то может в ноль свалиться?

[VoloCh]

paha в сообщении #307677 писал(а):

я перестал за топиком следить...

VoloCh в сообщении #306783 писал(а):

Если есть контрпример, то для этого примера, очевидно, $\beta_n\to\alpha$

а вот почему?

Ну, как, ведь $r_n\to\infty$ (в контрпримере), а при этом поворот остается тот же, значит, проекционная поправка (максимум вектором $(\frac12,\frac12)$) "деленная" на этот $r_n$, стремится к 0.

paha в сообщении #307677 писал(а):

разве кто-то может в ноль свалиться?

... эээ не знаю точно,... но при малых радиусах начальных вроде возможно... (надо подумать)

[Circiter]

2paha

Цитата:

разве кто-то может в ноль свалиться?

Конечно, при некоторых способах округления траектория коллапсирует. Представьте, к примеру, что начальная точка уже находится около нуля и при этом, после поворота на малюсенький угол, ей внезапно покоординатно trunc начинают делать... :)

2VoloCh

Цитата:

Я, извините, не понял вопроса. Угол поворота (по основной задаче) - строгая константа. Конечно, округление этот угол чуток подправит. И чем больше начальный радиус, тем эта поправка меньше.

Простите, я имел ввиду вот что. В ваших обозначениях одна из "веток" траектории частицы выглядит в полярных координатах как последовательность $\{r_n,\ \beta_n\}$, причем подразумевается, что точка $(r_i,\ \beta_i)$ под действием поворота $F_\alpha$ и округления $P$ переходит в $(r_{i+1},\ \beta_{i+1})\in PF_\alpha(r_i,\ \beta_i)$. Под угловым пробегом я понимаю величину $\mathcal{A}=\sum_i\triangle\varphi_i$, где $\triangle\varphi_i=\beta_i-\beta_{i-1}$. То есть я предложил такую гипотезу: последовательность $\triangle\varphi_i$ имеет вид:

• $0,\ 0,\ \ldots$
• или $\triangle\varphi_1,\ \ldots,\ \triangle\varphi_k,\ 0,\ 0,\ \ldots$ при $\triangle\varphi_i>0$ для $i\in[1;\ k]\subset\mathbb{N}$
• или просто $\forall\ i\in\mathbb{N}\ \triangle\varphi_i>0$

Ну или что-то вроде того... Что вы об этом думаете?

[Circiter]

Захотелось мне что-то провести небольшую "ревизию" условия задачи. Вот, например, paha требовал корректного определение оператора округления. Давайте попробуем подобрать что-нибудь подходящее.

Каким свойствам должен удовлетворять "округлятор" $P:\ \mathbb{R}^2\to\mathbb{Z}^2$? Понятно, что он должен оставлять неподвижными точки $\mathbb{Z}^2$, то есть действовать как метрический проектор $P^2=P$. Также ясно, что в общем случае $P$ -- многозначное отображение (ой!). Кстати, далее, при работе с многозначными функциями будет подразумеваться возможность поточечного применения функции к подмножеству области определения с объединением полученных образов (вполне естественная договоренность).

Произвольности выбора алгоритма округления хорошо отвечает "округлятор" сопоставляющий точке из $\mathbb{R}^2$ вершины содержащего её целочисленного квадратика -- фундаментального параллелограмма ортогональной $\mathbb{Z}^2$; другими словами, округлятор должен покоординатно округлять точку всеми возможными способами. Назовем такой округлятор сильным. Сходимость траекторий при использовании сильного округлятора, сдается мне, тесно связана со структурой $\mathbb{S}^1\cup\mathbb{Z}^2$, вернее, с распределением целочисленных точек на окружностях, а распределение это вовсе нетривиально, e.g. на окружности радиуса 350 лежат аж 60 таких точек и х.з., что они там делают. :) Кажется, Sonic86 рассуждал на эту тему, так что хотелось бы от него какие-нибудь комментарии услышать...

В принципе, такой округлятор очень удобен, например, у него (в композиции с $F_\alpha$) вроде бы нет равновесных точек. Но если удастся доказать сходимость любой траектории при использовании именно сильного округлятора, то это будет настоящим чудом!

Более же простой округлятор, -- назовем его слабым, -- напрямую соответствует требованию округления до ближайшей точки решетки. Его можно определить или через козякиновский round или например как

$$Px=\{z\in\mathbb{Z}^2\colon\|x-z\|=\inf_{p\in\mathbb{Z}^2}\|x-p\|\}.$$

Шансов сойтись у траектории слабого округлятора гораздо больше, но и сценариев такой сходимости тоже больше, что уже не так хорошо. Например эволюция системы может внезапно остановиться в некоторой точке равновесия.

Во всяком случае, предлагаю пока иметь дело именно со слабым округлятором.

В принципе, поведение системы видимо очень сильно зависит от конкретных свойств округлятора. Легко придумать похожую динамическую систему, основанную также на неточных поворотах, которая будет, к примеру, заведомо сходиться, или наоборот, расходиться, причем с очевидностью... На ум сразу же приходит проблема численного интегрирования уравнения $\dot x=-kx$, при котором вместо окружностей может получиться раскручивающаяся до бесконечности спираль.

Причина расхождения траектории по спирали к бесконечности при грубом интегрировании $\dot x=-kx$, например методом Эйлера, кроется в продвижении интегратора на каждом элементарном временном промежутке вдоль направленных от нуля касательных к концентрическим окружностям суть настоящим интегральным кривым этого дифура.

Конечно, это всего-лишь пример, имеющий мало общего с поворотами на решетке, при которых существенна анизотропия дискретного пространства... Так что поехали дальше. :)

Небольшое замечание. Всегда можно считать начальное состояние подмножеством решетки, ведь даже если начальная точка не принадлежит решетке, то не составит труда первую итерацию (поворот/округление) расчитать вручную.

В первую очередь мне захотелось исследовать неподвижные точки оператора $PF_\alpha$. К сожалению, эта чрезвычайно интересная тема для меня является terra incognita и мне пришлось искать подходящие теоремки и даже выдумывать кое-какие велосипеды. Мое внимание привлекла очень красивая теоремка Кнастера-Тарского о неподвижных точках монотонных отображений на решетках, в отличии от многих других подобных теорем не требующая сжимающих свойств оператора эволюции, его непрерывности или однозначности (впервые я о ней узнал совсем недавно, из небезызвестной статьи V.Deolalikar, $\mathrm{P}\neq\mathrm{NP}$ :) ). А так как её разбора я на этом форуме не нашел, соответствующие рассуждения-доказательства приведу прямо здесь (не удержался); может быть эти идеи и сподвигнут кого-нибудь на нормальное решение. :)

Пусть булеан над решеткой (сеткой) $\mathbb{Z}^2$ будет обозначен как $\mathfrak{L}\equiv\wp(\mathbb{Z}^2)$; кроме того, для краткости, "переобозначим" оператор $PF_\alpha$ как $f$, воспринимая $f$ как отображение $\mathfrak{L}$ в себя. Ключевым моментом является простой факт: $(\mathfrak{L},\ \subseteq)$ -- полная решетка (см. уточнение), то есть для любого подмножества $L\subseteq\mathfrak{L}$ определены супремум и инфимум через объединение и пересечение элементов, соответственно.

Функция $f$ монотонна. Под монотонностью подразумевается свойство сохранения отношения включения:

$$\forall\ x,\ y\in\mathfrak{L}\quad x\subseteq y\Rightarrow f(x)\subseteq f(y).\eqno(1)$$

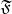
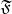
Множество $\mathfrak{F}$ содержит все неподвижные точки $f$, т.е., $\mathfrak{F}\equiv\{x\in\mathfrak{L}\ \mid\ f(x)=x\}$. Утверждается, что $\mathfrak{F}$ является полной решеткой; а доказательсво выглядит примерно так. Введем ещё одно вспомогательное множество $\mathfrak{U}\equiv\{x\in\mathfrak{L}\ \mid\ x\subseteq f(x)\}$. Для любого $x\in\mathfrak{U}$ выполняется $x\subseteq\sup\mathfrak{U}$ (что очевидно), а значит, в силу монотонности $f$, справедливо $f(x)\subseteq f(\sup\mathfrak{U})$.

По определению $\mathfrak{U}$, верно $x\subseteq f(x)$; получается, что $x\subseteq f(x)\subseteq f(\sup\mathfrak{U})$, из чего следует $x\subseteq f(\sup\mathfrak{U})$. Другими словами, все элементы $\mathfrak{U}$ "меньше" $f(\sup\mathfrak{U})$, то есть $f(\sup\mathfrak{U})$ -- верхняя грань $\mathfrak{U}$ (N.B., не супремум, а просто верхняя грань). Сам же $\sup\mathfrak{U}$ по определению супремума является наименьшей верхней гранью и не может "превышать" любую другую верхнюю грань:

$$\sup\mathfrak{U}\subseteq f(\sup\mathfrak{U}),\eqno(2)$$

причем из определения $\mathfrak{U}$ теперь понятно, что

$$\sup\mathfrak{U}\in\mathfrak{U}.\eqno(3)$$

Так как $x\in\mathfrak{U}$, то $x\subseteq f(x)$, а монотонность позволяет применить $f$ к обеим частям этого выражения: $f(x)\subseteq f(f(x))$; при этом становится видно, что $f(x)\in\mathfrak{U}$. Поэтому, с учетом $(3)$: $f(\sup\mathfrak{U})\in\mathfrak{U}$ и, как следствие, $f(\sup\mathfrak{U})\subseteq\sup\mathfrak{U}$. Последнее выражение вместе с $(2)$ приводят к выводу о неподвижности $\sup\mathfrak{U}$ относительно $f$, $f(\sup\mathfrak{U})=\sup\mathfrak{U}$.

Понятно, что $\mathfrak{F}\subseteq\mathfrak{U}$, т.е. $\mathfrak{U}$ содержит в том числе и все неподвижные точки $f$. Таким образом $\sup\mathfrak{U}$ является наибольшей неподвижной точкой исследуемой функции, $\sup \mathfrak{F}=\sup\mathfrak{U}\in \mathfrak{F}$.

Аналогичные рассуждения можно провести и с дуальной решеткой $(\mathfrak{L},\ \supseteq)$, которая тоже полна и на которой $f$ тоже монотонна. В результате должен получиться симметричный вывод о существовании наименьшей неподвижной точки

$$\inf \mathfrak{F}=\inf{\mathfrak{U}'}\in \mathfrak{F},\eqno(4)$$

где $\mathfrak{U}'\equiv\{x\in\mathfrak{L}\ \mid\ x\supseteq f(x)\}$.

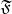
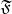
Теперь несколько слов о полноте $\mathfrak{F}$. Зафиксируем произвольное $W\subseteq \mathfrak{F}$ и выберем произвольный $x\in W$. Cправедливо $x\subseteq\sup W$, а значит и $f(x)\subseteq f(\sup W)$, но так как $\mathfrak{F}$ -- множество неподвижных точек, то $x=f(x)$, и получается, что $x\subseteq f(\sup W)$, т.е. $f(\sup W)$ -- верхняя грань $W$. Из этого вытекает

$$\sup W\subseteq f(\sup W).\eqno(5)$$

Определим отрезок $\mathfrak{D}\equiv\{z\in\mathfrak{L}\ \mid\ \sup W\subseteq z\subseteq \sup\mathfrak{L}\}$. Произвольно выберем $y\in\mathfrak{D}$, при этом конечно же $\sup W\subseteq y$. Монотонность $f$ позволяет переписать это выражение как $f(\sup W)\subseteq f(y)$, причем из последнего и из $(5)$ следует, что $\sup W\subseteq f(y)$, то есть $f(x)\in\mathfrak{D}$. Это позволяет ввести функцию $f'$, ограничив область определения $f$ на отрезок $\mathfrak{D}$ (заметьте, $f'$ здесь тоже будет монотонной).

Фактически, коль скоро наш отрезок является полной решеткой, а $f'$ монотонной функцией на нем, то к этим объектам мы можем применить уже полученные выше результаты и утверждать, что согласно $(4)$, $f'$ имеет здесь наименьшую неподвижную точку (которая является неподвижной и для $f$, разумеется). Так как эта точка находится на отрезке $\mathfrak{D}$, то она является верхней гранью для $W$. А раз уж она наименьшая среди всех других неподвижных точек на том же отрезке, то выходит, что найденная неподвижная точка равна $\sup W$ (важно помнить, что $W\subseteq \mathfrak{F}$).

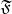
Итак, произвольное $W$ имеет супремум. Используя уже знакомый прием с применением дуальных решеток, по аналогии устанавливается существование инфимума. Значит $W$ -- полная решетка, а из произвольности выбора этого подмножества следует полнота решетки $\mathfrak{F}$, в частности её непустота.

Выберем произвольное непустое подмножество $\mathcal{Z}\subset\mathbb{Z}^2$. Сконструируем оператор $\mathcal{R}\colon\wp(\mathbb{Z}^2)\to\wp(\mathbb{Z}^2)$, такой что $\mathcal{R}(\varnothing)\equiv\mathcal{Z}$ и $\mathcal{R}(x)\equivf(x)$. Этот оператор вроде-бы обладает монотонностью:

$$\forall\ x,\ y\subset\mathbb{Z}^2\quad x\subseteq y\Rightarrow\mathcal{R}(x)\subseteq\mathcal{R}(y).\eqno(6)$$

Траекторией $\mathcal{R}$ будет последовательность $x_i$, в которой $x_0\equiv\infty$, а все следующие элементы выглядят как $x_{i+1}\equiv\mathcal{R}(x_i)$. Видно, что $x_0\subseteq x_1$. Монотонность $\mathcal{R}$ позволяет применить его к обеим частям этого выражения, $\mathcal{R}(x_0)\subseteq\mathcal{R}(x_1)$, которое теперь, очевидно, равно $x_1\subseteq x_2$. По-индукции,

$$x_i\subseteq x_{i+1}.\eqno(7)$$

Это свойство позволяет выразить предел последовательности через объединение её элементов:

$$x_\infty\equiv\lim_{i\to\infty}{x_i}=\bigcup_{i=0}^\infty{x_i}.$$

Оператор $\mathcal{R}$ имеет ещё одно замечательное свойство -- он дистрибутивен относительно объединения:

$$\mathcal{R}\left(\bigcup_i z_i\right)=\bigcup_i{\mathcal{R}(z_i)}.\eqno(8)$$

Применим $\mathcal{R}$ к $x_\infty$:

$$\begin{align}\mathcal{R}(x_\infty)&=\mathcal{R}\left(\bigcup_{i=0}^\infty{x_i}\right)=\bigcup_{i=0}^\infty{\mathcal{R}(x_i)}=\\ &=\varnothing\cup\bigcup_{i=0}^\infty{x_{i+1}}=x_0\cup\bigcup_{i=1}^\infty{x_i}=\bigcup_{i=0}^\infty x_i=x_\infty.\end{align}$$

То есть, $x_\infty$ -- неподвижная точка $\mathcal{R}$.

Внимание, положения $(1,\ 6-8)$ остро нуждаются в доказательстве и комментариях! Но это ещё пол-беды, дальше выкладки будут ещё бредовее. :)

В силу $(6)$ и в свете ранее доказанного, оператор $\mathcal{R}$ имеет наименьшую неподвижную точку $x^*$. Это можно записать как $x^*=\mathcal{R}(x^*)$, но можно к правой части применить $\mathcal{R}$ сколько угодно раз, например так: $x^*=\mathcal{R}^n(x^*)$. Очевидно, ничего не изменится если приписать к правой части символ объединения (ведь $x^*$ все-равно неподвижна):

$$x^*=\bigcup_{i=0}^\infty{\mathcal{R}^i(x^*)}.$$

Дальше интересней:

$$\begin{align}x^*=\bigcup_{i=0}^\infty{\mathcal{R}^i(x^*\cup\varnothing)}&=\bigcup_{i=0}^\infty{\Big(\mathcal{R}^i(x^*)\cup\mathcal{R}^i(\varnothing)\Big)}=\\ &=\bigcup_{i=0}^\infty{\mathcal{R}^i(x^*)}\cup\bigcup_{i=0}^\infty{\mathcal{R}^i(\varnothing)}.\end{align}$$

То есть, получается, что $x^*=x^*\cup x_\infty$. Вроде-бы это возможно только если $x_\infty\subseteq x^*$, но, как было установлено выше, $x_\infty$ есть неподвижная точка $\mathcal{R}$, а $x^*$ -- его наименьшая неподвижная точка. Поэтому $x^*=x_\infty$, т.е. монотонность на полной решетке гарантирует существование неподвижной точки, а дистрибутивность дает конструктивный способ её нахождения путем итерирования оператора $\mathcal{R}$ с "отталкиванием" от произвольного $\mathcal{Z}$.

Увы, в отжигах самого Тарского последний результат-рецепт мне найти не удалось, а у Деолаликара есть только упоминание, без объяснений (на список литературы я особо не набрасывался).

Но все равно, как вам такой аргумент по Кнастеру-Тарскому в пользу сходимости любой траектории у рассматриваемой в данной теме динамической системы? Можно ли как-нибудь развить этот подход и получить конкретные, экспериментально проверяемые параметры аттрактора, например его диаметры?

[Circiter]

Опечатка: подразумевалось $\mathcal{R}(\varnothing)\equiv\mathcal{Z}$, $\mathcal{R}(x)\equiv f(x)$.

-- Вс ноя 07, 2010 01:33:44 --

Опа, странность одна имеется... Что если вместо $\mathbb{Z}^2$ взять континуум $\mathbb{R}^2$, а вместо $PF_\alpha$ взять просто $F_\alpha$ с иррациональным $\alpha$. Вроде-бы соображения по Кнастеру-Тарскому здесь тоже применимы, но ведь орбита такой динамической системы всюду плотна и построить её за конечное время невозможно (хотя она и остается ограниченной по удаленности от нуля). Где-же здесь нарушаются условия теоремы?..