решить уравнение Yoshio Koide в натуральных числах

[Аурелиано Буэндиа]

В физике встречается формула Ёшио Койде

$$ \frac{x+y+z}{(\sqrt{x}+\sqrt{y}+\sqrt{z})^2}=\frac{2}{3}. $$

Возник вопрос, а дупускает ли это уравнение решение в натуральных числах $x<y<z$?

[juna]

Вроде нет решений, т.к. неразрешимо сравнение $x^2+y^2+z^2=0\mod4}$ при взаимнопростых $x,y,z$, хотя надо повнимательнее посмотреть

[Борис Лейкин]

Аурелиано Буэндиа писал(а):

В физике встречается формула Ёшио Койде

А где в физике она встречается, извините?

[Руст]

Уравнение в целых числах сводится к решению в целых числах следующего уравнения: $a^2+b^2=3c^2$, которое очевидно не имеет решения (в левой части 3 может входить только в чётной степени, в правой нечётной).

[Аурелиано Буэндиа]

Руст писал(а):

Уравнение в целых числах сводится к решению в целых числах следующего уравнения: $a^2+b^2=3c^2$, которое очевидно не имеет решения (в левой части 3 может входить только в чётной степени, в правой нечётной).

Руст, я не силен в теории чисел, поэтому поясните, пожалуйста, почему в левой части 3 может входить только в четной степени? С правой частью мне все понятно.
У меня тоже получалось такое равенство, когда я делал замену

$$ x=\left(a+2c-\frac{2}{3}b\right)^2,\ \ y=\left(c-\frac{2}{3}b\right)^2,\ \ z=\left(\frac{b}{3}\right)^2. $$

т.е. я рассматривал $x,y,z$ как квадраты рациональных чисел. Но мне кажется, что множество квадратов натуральных чисел не равно множеству натуральных чисел. Если это так, то этот путь не гарантирует отсутствие натуральных решений у уравнения.

Борис Лейкин, посмотрите википедию.

[Аурелиано Буэндиа]

Артамонов Ю.Н. писал(а):

Вроде нет решений, т.к. неразрешимо сравнение $x^2+y^2+z^2=0\mod4}$ при взаимнопростых $x,y,z$, хотя надо повнимательнее посмотреть

Это что-то умное и не очень понятное.

[незваный гость]

Пусть тройка $a$, $b$, $c$ несократима. Тогда:
$a^2+b^2= 3 c^2 \Rightarrow $ $a^2+b^2 \dot: 3 \Rightarrow$ (рассмотрев остатки квадратов по модулю 3) $a \dot: 3 \wedge b \dot: 3 \Rightarrow$ $a^2+b^2 \dot: 9 \Rightarrow$ $c \dot: 3$.

[juna]

Аурелиано Буэндиа писал(а):

Артамонов Ю.Н. писал(а):

Вроде нет решений, т.к. неразрешимо сравнение $x^2+y^2+z^2=0\mod4}$ при взаимнопростых $x,y,z$, хотя надо повнимательнее посмотреть

Это что-то умное и не очень понятное.

Да ничего хитрого здесь нет, все даже более непосредственно вытекает: вместо $x,y,z$ вводим $a^2=x,b^2=y,c^2=z$. Тогда уравнение сведется к $\frac{a^2+b^2+c^2}{(a+b+c)^2}=\frac{2}{3}$. После преобразований имеем $4(ab+ac+bc)=a^2+b^2+c^2$. Далее заметим, что есть смысл рассматривать только взаимнопростые решения, значит $(a,b)=1, (b,c)=1, (a,c)=1$. Перебирая все возможные остатки выражения $a^2+b^2+c^2$ при взаимнопростых $a,b,c$ по модулю 4 убеждаемся, что решений нет. Только я чего-нибудь мог пропустить в этом переборе, поэтому говорил, что нужно повнимательнее посмотреть. Может сами попробуете.

[Руст]

Да это так же проходит. Единственное осталось показать, что если

$$\sum_{k=1}^n \sqrt{r_k}=q\Longrightarrow \sqrt{r_i}=q_i.$$

Здесь все переменные рациональные числа.
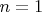
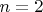
Это известная олимпиадная, для $n<6$ можно легко доказать школьными методами. При $n=1$ доказывать ничего. При $n=2$ перенесём первую переменную направо и возведём в квадрат и отсюда получим, что квадратный корень от первого числа рациональное, а следовательно это верно и для второго. При $n=3$ поступим так же и получим, сумма двух квадратных корней от рациональных чисел равно рациональному, т.е. пришли к $n=2$. 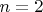Одно из них наша переменная, значит сумма и двух исходных квадратных переменных рациональное. 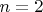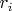Ещё раз ссылаясь к $n=2$ получим все $r_i$ квадраты рациональных чисел. Так как ваше уравнение однородное, то приводя к общему знаменателю приводится к решению в целых числах.
Что касается того, что из $p|x^2+y^2>0\Longrightarrow ord_p(x^2+y^2)-even \ or \ p=1\pmod 4$ я считал всем известным. Я когда то объяснял это семикласснику.
Так что ваше уравнение не имеет решения в рациональных числах.