День добрый!
Для решения некой физической задачи хочу программно построить двумерные функции Эрмита-Гаусса для комплексных чисел
(Довольно подробное описание дано, например, здесь:
http://www.fian.smr.ru/img_beam/Vestnik.djv)
Прежде чем сформулировать вопрос, поясню:
Для одномерного случая полиномы Эрмита можно построить, используя рекурентное соотношение



Для этого я циклом сначала задавал переменную

в каком-то диапазоне,
затем полученный массив

использовал для вычисления полиномов.
В итоге получался двумерный массив, в котором были определены значения для каждого из

полиномов для каждого из

Функции Э-Г для вещественных чисел можно построить, если вычислим полиномы для второй координаты

, и перемножим их по правилу:

получается четырехмерный массив, если зафиксируем
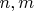
, и возведем массив в квадрат, его можно представить графически как интенсивность.
Например, при значении

, получим "интенсивность", показанную слева в верхнем ряду на прикрепленном рисунке,

- изображение сверху в центре, и т.д.
Вопрос состоит в том - как получить соответсвующие им "фазы", вида

, (нижний ряд на рисунке)

По моим соображениям, для этого нужно задать еще одну ось, скажем,

, так, что

будет комплексным числом.
для них построить полиномы эрмита, и опираясь на них построить функции эрмита-Гаусса
А потом разделить на вещественные и комплексные части
Непонято, как именно строить полиномы Эрмита от комплексного числа. Задавать вместо оси

плоскость

?
Тогда циклов становится слишком много, и программа ругается - что нехватает памяти.
и как потом отделять вещественную часть от мнимой?
или же можно отдельно подсчитать вещественную часть, отдельно мнимую?



